
【题目】已知向量 ![]() ,
, ![]() ,设
,设 ![]() .
.
(Ⅰ)若f(α)=2,求 ![]() 的值;
的值;
(Ⅱ)在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a﹣b)cosC=ccosB,求f(A)的取值范围.
【答案】解:(Ⅰ)向量 ![]() ,
, ![]() ,
,
∵ ![]()
那么: ![]() =
= ![]() =
= ![]() .
.
∵f(α)=2,即 ![]() =
= ![]() ,
,
∴ ![]() .
.
(Ⅱ)∵(2a﹣b)cosC=ccosB,
∴(2sinA﹣sinB)cosC=sinCcosB,
2sinAcosC=sinBcosC+cosBsinC=sin(B+C),
∴2sinAcosC=sinA,
∵sinA≠0,
∴ ![]() ,∴
,∴ ![]() .
.
∴ ![]() ,
,
![]() ,
,
∴ ![]() ,
,
∵ ![]() ,
,
∴f(A)的取值范围为(2,3).
【解析】(Ⅰ)根据题意由两个向量的数量积运算公式可得出 f ( x )的解析式,结合已知利用余弦函数二倍角的关系式式即可求出结果。(Ⅱ)利用正弦定理结合两角和差的正弦公式即可得出2sinAcosC=sinA,进而可得出 cosC的值 故可求出角A的大小,再由已知角的取值范围得出![]() 的取值范围进而求出 f ( A ) 的取值范围即可。
的取值范围进而求出 f ( A ) 的取值范围即可。


科目:高中数学 来源: 题型:
【题目】函数f(x)= 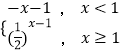 的图象与函数g(x)=log2(x+a)(a∈R)的图象恰有一个交点,则实数a的取值范围是( )
的图象与函数g(x)=log2(x+a)(a∈R)的图象恰有一个交点,则实数a的取值范围是( )
A.a>1
B.a≤﹣ ![]()
C.a≥1或a<﹣ ![]()
D.a>1或a≤﹣ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在一个坡度一定的山坡AC的顶上有一高度为25m的建筑物CD,为了测量该山坡相对于水平地面的坡角θ,在山坡的A处测得∠DAC=15°,沿山坡前进50m到达B处,又测得∠DBC=45°,根据以上数据可得cosθ= . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若幂函数f(x)的图象过点 ![]() ,则函数g(x)=exf(x)的单调递减区间为( )
,则函数g(x)=exf(x)的单调递减区间为( )
A.(-∞,0)
B.(-∞,-2)
C.(-2,-1)
D.(-2,0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ln(1+x)+mln(1-x)是偶函数,则( )
A.m=1,且f(x)在(0,1)上是增函数
B.m=1,且f(x)在(0,1)上是减函数
C.m=-1,且f(x)在(0,1)上是增函数
D.m=-1,且f(x)在(0,1)上是减函数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com