【题目】若幂函数f(x)的图象过点 
，则函数g(x)＝exf(x)的单调递减区间为( )
A.(－∞，0)
B.(－∞，－2)
C.(－2，－1)
D.(－2,0)
【答案】D
【解析】设幂函数f(x)＝xα ， 因为图象过点 
，所以 
＝ 
α ， α＝2，所以f(x)＝x2 ， 故g(x)＝exx2 ， 令g′(x)＝exx2＋2exx＝ex(x2＋2x)＜0，得－2＜x＜0，故函数单调减区间为(－2,0)
故答案为：D.先求幂函数f（x），再利用导数判定函数g（x）的单调递减区间．导数和函数的单调性的关系：
（1）若f′（x）＞0在（a，b）上恒成立，则f（x）在（a，b）上是增函数，f′（x）＞0的解集与定义域的交集的对应区间为增区间；
（2）若f′（x）＜0在（a，b）上恒成立，则f（x）在（a，b）上是减函数，f′（x）＜0的解集与定义域的交集的对应区间为减区间．
单元加期末复习先锋大考卷系列答案
出彩同步大试卷系列答案科目：高中数学 来源： 题型：
【题目】函数f（x）=（x﹣2）（ax+b）为偶函数，且在（0，+∞）单调递增，则f（2﹣x）＞0的解集为（ ）
A.{x|x＞2或x＜﹣2}
B.{x|﹣2＜x＜2}
C.{x|x＜0或x＞4}
D.{x|0＜x＜4}
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f(x)＝ex－e－x(x∈R，且e为自然对数的底数).
（1）判断函数f(x)的单调性与奇偶性；
（2）是否存在实数t ， 使不等式f(x－t)＋f(x2－t2)≥0对一切x∈R都成立？若存在，求出t；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在等腰直角△ABO中，设 
= 
， 
= 
，| |=| |=1，C为AB上靠近A点的三等分点，过C作AB的垂线l，设P为垂线上任一点， 
= 
，则 （ ﹣ ）=（ ） 
A.
B.﹣
C.﹣ 
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知向量 
， 
，设 
．
（Ⅰ）若f（α）=2，求 
的值；
（Ⅱ）在△ABC中，角A，B，C的对边分别是a，b，c，且满足（2a﹣b）cosC=ccosB，求f（A）的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某人到甲、乙两市各 
个小区调查空置房情况，调查得到的小区空置房的套数绘成了如图的茎叶图，则调查中甲市空置房套数的中位数与乙市空置房套数的中位数之差为（ ）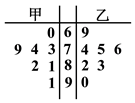
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图， 
为圆柱 
的母线， 
是底面圆 
的直径， 
是 
的中点.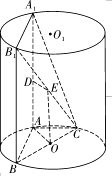
（Ⅰ）问： 
上是否存在点 
使得 
平面 
？请说明理由；
（Ⅱ）在（Ⅰ）的条件下，若 
平面 
，假设这个圆柱是一个大容器，有条体积可以忽略不计的小鱼能在容器的任意地方游弋，如果小鱼游到四棱锥 
外会有被捕的危险，求小鱼被捕的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对于椭圆 
，有如下性质：若点 
是椭圆上的点，则椭圆在该点处的切线方程为 
.利用此结论解答下列问题.
（Ⅰ）求椭圆 
的标准方程；
（Ⅱ）若动点 
在直线 
上，经过点 的直线 
与椭圆 相切，切点分别为 
.求证直线 
必经过一定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com