Question

【题目】如图， 为圆柱 的母线， 是底面圆 的直径， 是 的中点.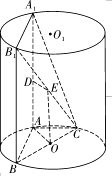

（Ⅰ）问： 上是否存在点 使得 平面 ？请说明理由；
（Ⅱ）在（Ⅰ）的条件下，若 平面 ，假设这个圆柱是一个大容器，有条体积可以忽略不计的小鱼能在容器的任意地方游弋，如果小鱼游到四棱锥 外会有被捕的危险，求小鱼被捕的概率.

Answer 1

【答案】解：（Ⅰ）存在，E是 的中点．
证明：如图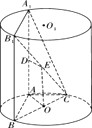

连接 , ∵ 分别为 , 的中点，
∴ ，
又 ，且 ，
∴四边形 是平行四边形，
即 , 平面 , 平面 ，
∴ 平面 .
（Ⅱ）鱼被捕的概率 ，
由 平面 ，且由（Ⅰ）知 ，∴ 平面 ，∴ ，
又 是 中点，∴ ，因 是底面圆 的直径，得 ，且 ，
∴ 平面 ，即 为四棱锥 的高．
设圆柱高为 ，底面半径为 ，则 ，
，
∴ .
故答案为： ．
【解析】（1）要使CB1上存在点点 E 使得 DE / / 平面 ABC，则当点E为CB1的中点时，四边形 AOED 是平行四边形，能满足D E / / 平面 ABC.
（2）这是一个概型问题，由体积的比值求出概率，本题适合间接法.