练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知 则方程 的根的个数为（ ）
    A.5
    B.4
    C.1
    D.无数多个

    【答案】B
    【解析】结合函数的解析式可知，当 时， ，
    将函数在区间 上的图象向左平移 个单位即可得到函数在区间 上的图象；
    同样的方法，向右平移 次即可得到函数 的图象，
    然后绘制函数 的图象，观察可得，函数 与函数 的交点的个数为 个，
    则方程 的根的个数为4个.
    所以答案是：B.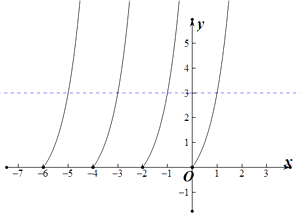

    【考点精析】掌握函数的零点与方程根的关系和函数的零点是解答本题的根本，需要知道二次函数的零点：（1）△＞0，方程 有两不等实根，二次函数的图象与 轴有两个交点，二次函数有两个零点;（2）△＝0，方程 有两相等实根（二重根），二次函数的图象与 轴有一个交点，二次函数有一个二重零点或二阶零点;（3）△＜0，方程 无实根，二次函数的图象与 轴无交点，二次函数无零点；函数的零点就是方程的实数根，亦即函数的图象与轴交点的横坐标．即：方程有实数根，函数的图象与坐标轴有交点，函数有零点．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知x0是f(x)＝ 的一个零点，x1∈(－∞，x0)，x2∈(x0,0)，则( )
    A.f(x1)＜0，f(x2)＜0
    B.f(x1)＞0，f(x2)＞0
    C.f(x1)＞0，f(x2)＜0
    D.f(x1)＜0，f(x2)＞0

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若方程kx－ln x＝0有两个实数根，则k的取值范围是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列函数为奇函数的是( )
    A.y＝x3＋3x2
    B.y＝
    C.y＝xsin x
    D.y＝

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图， 为圆柱 的母线， 是底面圆 的直径， 是 的中点.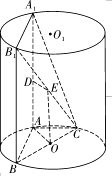

    （Ⅰ）问： 上是否存在点 使得 平面 ？请说明理由；
    （Ⅱ）在（Ⅰ）的条件下，若 平面 ，假设这个圆柱是一个大容器，有条体积可以忽略不计的小鱼能在容器的任意地方游弋，如果小鱼游到四棱锥 外会有被捕的危险，求小鱼被捕的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

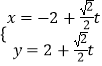    【题目】已知曲线 的参数方程为 （ 为参数），直线 的参数方程为 （ 为参数）.
    （Ⅰ）求曲线 和直线 的普通方程；
    （Ⅱ）若点 为曲线 上一点，求点 到直线 的距离的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程
    在直角坐标系 中，直线 的参数方程为 （ 为参数），直线 的参数方程为 （ 为参数），设 与 的交点为 ，当 变化时， 的轨迹为曲线 .
    （1）写出 的普遍方程及参数方程；
    （2）以坐标原点为极点， 轴正半轴为极轴建立极坐标系，设曲线 的极坐标方程为 ， 为曲线 上的动点，求点 到 的距离的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系 中，以原点 为极点，以 轴正半轴为极轴，圆 的极坐标方程为 ．
    （1）将圆 的极坐标方程化为直角坐标方程；
    （2）过点 作斜率为1直线 与圆 交于 两点，试求 的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆 的离心率为 ，且椭圆 过点 ，直线 过椭圆 的右焦点 且与椭圆 交于 两点.
    (Ⅰ)求椭圆 的标准方程；
    (Ⅱ)已知点 ，求证：若圆 与直线 相切，则圆 与直线 也相切.

    查看答案和解析>>

    同步练习册答案