
【题目】已知椭圆 ![]() 的离心率为
的离心率为 ![]() ,且椭圆
,且椭圆 ![]() 过点
过点 ![]() ,直线
,直线 ![]() 过椭圆
过椭圆 ![]() 的右焦点
的右焦点 ![]() 且与椭圆
且与椭圆 ![]() 交于
交于 ![]() 两点.
两点.
(Ⅰ)求椭圆 ![]() 的标准方程;
的标准方程;
(Ⅱ)已知点 ![]() ,求证:若圆
,求证:若圆 ![]() 与直线
与直线 ![]() 相切,则圆
相切,则圆 ![]() 与直线
与直线 ![]() 也相切.
也相切.
【答案】解:(Ⅰ)设椭圆C的焦距为2c(c>0),依题意, 
解得 ![]() ,c=1,故椭圆C的标准方程为
,c=1,故椭圆C的标准方程为 ![]() ;
;
(Ⅱ)证明:当直线l的斜率不存在时,直线l的方程为 ![]() ,M , N两点关于x轴对称,点P(4,0)在x轴上,所以直线PM与直线PN关于x轴对称,所以点O到直线PM与直线PN的距离相等,故若圆
,M , N两点关于x轴对称,点P(4,0)在x轴上,所以直线PM与直线PN关于x轴对称,所以点O到直线PM与直线PN的距离相等,故若圆 ![]() 与直线PM相切,则也会与直线PN相切;
与直线PM相切,则也会与直线PN相切;
当直线l的斜率存在时,设直线l的方程为 ![]() ,
, ![]() ,
, ![]() ,
,
由  得:
得: ![]()
所以 ![]() ,
, ![]() ,
,![]() ,
, ![]() ,
,![]()
 ,
,
所以, ![]() ,于是点O到直线PM与直线的距离PN相等,
,于是点O到直线PM与直线的距离PN相等,
故若圆 ![]() 与直线PM相切,则也会与直线PN相切;
与直线PM相切,则也会与直线PN相切;
综上所述,若圆 ![]() 与直线PM相切,则圆
与直线PM相切,则圆 ![]() 与直线PN也相切
与直线PN也相切
【解析】(1)利用已知条件列出关于a、b的方程组,即可得到椭圆C的标准方程。(2)根据题意对直线的斜率分类讨论,若圆与直线相切等价于kPM+kPN=0联立方程借助韦达定理即可证明等式即可。
【考点精析】认真审题,首先需要了解椭圆的标准方程(椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() ).
).


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的四个顶点组成的四边形的面积为
的四个顶点组成的四边形的面积为 ![]() ,且经过点
,且经过点 ![]() .
.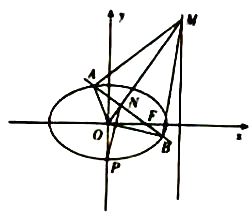
(1)求椭圆 ![]() 的方程;
的方程;
(2)若椭圆 ![]() 的下顶点为
的下顶点为 ![]() ,如图所示,点
,如图所示,点 ![]() 为直线
为直线 ![]() 上的一个动点,过椭圆
上的一个动点,过椭圆 ![]() 的右焦点
的右焦点 ![]() 的直线
的直线 ![]() 垂直于
垂直于 ![]() ,且与
,且与 ![]() 交于
交于 ![]() 两点,与
两点,与 ![]() 交于点
交于点 ![]() ,四边形
,四边形 ![]() 和
和 ![]() 的面积分别为
的面积分别为 ![]() .求
.求 ![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列命题:
①命题“ ![]() ,
, ![]() ”的否定是:“
”的否定是:“ ![]() ,
, ![]() ”;
”;
②若样本数据 ![]() 的平均值和方差分别为
的平均值和方差分别为 ![]() 和
和 ![]() 则数据
则数据 ![]() 的平均值和标准差分别为
的平均值和标准差分别为 ![]() ,
, ![]() ;
;
③两个事件不是互斥事件的必要不充分条件是两个事件不是对立事件;
④在 ![]() 列联表中,若比值
列联表中,若比值 ![]() 与
与 ![]() 相差越大,则两个分类变量有关系的可能性就越大.
相差越大,则两个分类变量有关系的可能性就越大.
⑤已知 ![]() 为两个平面,且
为两个平面,且 ![]() ,
, ![]() 为直线.则命题:“若
为直线.则命题:“若 ![]() ,则
,则 ![]() ”的逆命题和否命题均为假命题.
”的逆命题和否命题均为假命题.
⑥设定点 ![]() 、
、 ![]() ,动点
,动点 ![]() 满足条件
满足条件 ![]() 为正常数),则
为正常数),则 ![]() 的轨迹是椭圆.其中真命题的个数为( )
的轨迹是椭圆.其中真命题的个数为( )
A.5
B.4
C.3
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知 ![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 平面
平面 ![]() .
.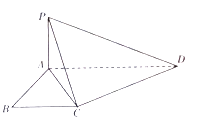
(Ⅰ) ![]() 上是否存在点
上是否存在点 ![]() 使
使 ![]() 平面
平面 ![]() ,若存在,指出
,若存在,指出 ![]() 的位置并证明,若不存在,请说明理由;(Ⅱ)证明:
的位置并证明,若不存在,请说明理由;(Ⅱ)证明: ![]() ;
;
(Ⅲ)若 ![]() ,求点
,求点 ![]() 到平面
到平面 ![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据《中华人民共和国道路交通安全法》规定:“车辆驾驶员血液酒精溶度(单位mg/100ml)/在![]() ,属于酒后驾驶;血液浓度不低于80,属于醉酒驾驶。”2017年“中秋节”晚9点开始,济南市交警队在杆石桥交通岗前设点,对过往的车辆进行检查,经过4个小时,共查处喝过酒的驾驶者60名,下图是用酒精测试仪对这60名驾驶者血液中酒精溶度进行检测后所得结果画出的频率分布直方图。
,属于酒后驾驶;血液浓度不低于80,属于醉酒驾驶。”2017年“中秋节”晚9点开始,济南市交警队在杆石桥交通岗前设点,对过往的车辆进行检查,经过4个小时,共查处喝过酒的驾驶者60名,下图是用酒精测试仪对这60名驾驶者血液中酒精溶度进行检测后所得结果画出的频率分布直方图。
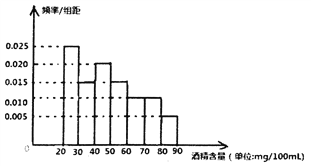
(1)求这60名驾驶者中属于醉酒驾车的人数(图中每组包括左端点,不包括右端点)
(2)若以各小组的中值为该组的估计值,频率为概率的估计值,求这60名驾驶者血液的酒精浓度的平均值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com