
【题目】已知x0是f(x)= ![]() 的一个零点,x1∈(-∞,x0),x2∈(x0,0),则( )
的一个零点,x1∈(-∞,x0),x2∈(x0,0),则( )
A.f(x1)<0,f(x2)<0
B.f(x1)>0,f(x2)>0
C.f(x1)>0,f(x2)<0
D.f(x1)<0,f(x2)>0
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知命题p:“存在x0∈[1,+∞),使得(log23) ![]() ≥1”,则下列说法正确的是( )
≥1”,则下列说法正确的是( )
A.p是假命题;¬p“任意x∈[1,+∞),都有(log23)x<1”
B.p是真命题;¬p“不存在x0∈[1,+∞),使得(log23) ![]() <1”
<1”
C.p是真命题;¬p“任意x∈[1,+∞),都有(log23)x<1”
D.p是假命题;¬p“任意x∈(﹣∞,1),都有(log23)x<1”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数 ![]() ,
, ![]() ,对于给定的非零实数
,对于给定的非零实数 ![]() ,总存在非零常数
,总存在非零常数 ![]() ,使得定义域
,使得定义域 ![]() 内的任意实数
内的任意实数 ![]() ,都有
,都有 ![]() 恒成立,此时
恒成立,此时 ![]() 为
为 ![]() 的类周期,函数
的类周期,函数 ![]() 是
是 ![]() 上的
上的 ![]() 级类周期函数.若函数
级类周期函数.若函数 ![]() 是定义在区间
是定义在区间 ![]() 内的2级类周期函数,且
内的2级类周期函数,且 ![]() ,当
,当 ![]() 时,
时, 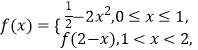 函数
函数 ![]() .若
.若 ![]() ,
, ![]() ,使
,使 ![]() 成立,则实数
成立,则实数 ![]() 的取值范围是( )
的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A.1盏
B.3盏
C.5盏
D.9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx+1(a,b为实数,a≠0,x∈R).
(1)若函数f(x)的图象过点(-2,1),且方程f(x)=0有且只有一个根,求f(x)的表达式;
(2)在(1)的条件下,当x∈[-1,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥 ![]() 中,底面梯形
中,底面梯形 ![]() ,
, ![]() ,平面
,平面 ![]() 平面
平面 ![]() ,
, ![]() 是等边三角形,已知
是等边三角形,已知 ![]() ,
, ![]() ,
, ![]() 是
是 ![]() 上任意一点,
上任意一点, ![]() ,且
,且 ![]() .
.
(1)求证:平面 ![]() 平面
平面 ![]() ;
;
(2)试确定 ![]() 的值,使三棱锥
的值,使三棱锥 ![]() 体积为三棱锥
体积为三棱锥 ![]() 体积的3倍.
体积的3倍.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的三个内角A,B,C的对边分别a,b,c,已知 ![]() ,
, ![]() ,且
,且 ![]() ∥
∥ ![]()
(1)证明sinBsinC=sinA;
(2)若a2+c2﹣b2= ![]() ac,求tanC.
ac,求tanC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com