练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】若函数f(x)＝－ x3＋ x2＋2ax在 上存在单调递增区间，则a的取值范围是 ．

    【答案】
    【解析】对f(x)求导，得f′(x)＝－x2＋x＋2a
    ＝－ 2＋ ＋2a.
    当x∈ 时，f′(x)的最大值为f′ ＝ ＋2a.
    令 ＋2a＞0，解得a＞－ .
    所以a的取值范围是 .
    求出函数的导数，利用导函数值大于0，转化为a的表达式，求出最值即可得到a的范围．导数和函数的单调性的关系：
    （1）若f′（x）＞0在（a，b）上恒成立，则f（x）在（a，b）上是增函数，f′（x）＞0的解集与定义域的交集的对应区间为增区间；
    （2）若f′（x）＜0在（a，b）上恒成立，则f（x）在（a，b）上是减函数，f′（x）＜0的解集与定义域的交集的对应区间为减区间．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥P﹣ABCD中，PA⊥底面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，N为PC的中点．
    （1）证明：MN∥平面PAB；
    （2）求直线AN与平面PMN所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知坐标平面上动点 与两个定点 ， ，且 .
    （1）求点 的轨迹方程，并说明轨迹是什么图形；
    （2）记（1）中轨迹为 ，过点 的直线 被 所截得的线段长度为8，求直线 的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知向量 ， ，设 ．
    （Ⅰ）若f（α）=2，求 的值；
    （Ⅱ）在△ABC中，角A，B，C的对边分别是a，b，c，且满足（2a﹣b）cosC=ccosB，求f（A）的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f(x)＝3x－x3在区间(a2－12，a)上有最小值，则实数a的取值范围是( )
    A.(－1,3)
    B.(－1,2)
    C.(－1,3]
    D.(－1,2]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某人到甲、乙两市各 个小区调查空置房情况，调查得到的小区空置房的套数绘成了如图的茎叶图，则调查中甲市空置房套数的中位数与乙市空置房套数的中位数之差为（ ）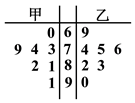

    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知矩形 所在平面与等腰直角三角形 所在平面互相垂直， ， ， 为线段 的中点．
    （Ⅰ）证明： ；
    （Ⅱ）求 与平面 所成的角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某化工厂为预测产品的回收率 ，需要研究它和原料有效成分含量 之间的相关关系，现收集了4组对照数据。

    3

    4

    5

    6

    2.5

    3

    4

    4.5

    （Ⅰ）请根据相关系数 的大小判断回收率 与 之间是否存在高度线性相关关系；
    （Ⅱ）请根据上表提供的数据，用最小二乘法求出 关于 的线性回归方程 ，并预测当 时回收率 的值.
    参考数据：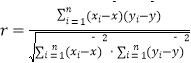

    1

    0

    其他

    相关关系

    完全相关

    不相关

    高度相关

    低度相关

    中度相关

    ，

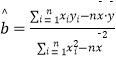    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 （ ）在同一半周期内的图象过点 ， ， ，其中 为坐标原点， 为函数 图象的最高点， 为函数 的图象与 轴的正半轴的交点， 为等腰直角三角形.

    （1）求 的值；
    （2）将 绕原点 按逆时针方向旋转角 ，得到 ，若点 恰好落在曲线 （ ）上（如图所示），试判断点 是否也落在曲线 （ ）上，并说明理由.

    查看答案和解析>>

    同步练习册答案