
分析 (1)如图所示,M(0,b),△MF1F2为正三角形.可得|MF1|=2|OF1|,即a=2c,可得椭圆离心率.
(2)由(1)可知:椭圆的方程化为:3x2+4y2=12c2.设直线AB的方程为ty=x-c,A(x1,y1),B(x2,y2).与椭圆的方程联立化为:(3t2+4)y2+6tcy-9c2=0,可得|y1-y2|=$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$.${S}_{△A{F}_{1}B}$=$\frac{1}{2}|{F}_{1}{F}_{2}|$•|y1-y2|=$\frac{12{c}^{2}\sqrt{{t}^{2}+1}}{3{t}^{2}+4}$.通过换元利用导数研究其单调性可得:△F1AB的面积取得最大值3c2.另一方面可得:设△F1AB的内切圆的半径为r,${S}_{△A{F}_{1}B}$=$\frac{1}{2}r×4a$≤3c2.可得r≤$\frac{3c}{4}$,利用$π×(\frac{3c}{4})^{2}$=$\frac{9π}{16}$,解得c即可得出.
解答 解:(1)如图所示,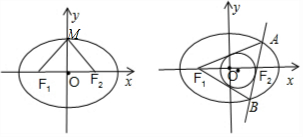
M(0,b),△MF1F2为正三角形.
∴|MF1|=2|OF1|,∴a=2c,
可得椭圆离心率e=$\frac{c}{a}$=$\frac{1}{2}$.
(2)由(1)可知:a=2c,b=$\sqrt{3}$c,
∴椭圆的方程化为:3x2+4y2=12c2.
设直线AB的方程为ty=x-c,A(x1,y1),B(x2,y2).
联立$\left\{\begin{array}{l}{ty=x-c}\\{3{x}^{2}+4{y}^{2}=12{c}^{2}}\end{array}\right.$,
化为:(3t2+4)y2+6tcy-9c2=0,
∴y1+y2=$\frac{-6tc}{3{t}^{2}+4}$,y1•y2=$\frac{-9{c}^{2}}{3{t}^{2}+4}$.
∴|y1-y2|=$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\frac{12c\sqrt{{t}^{2}+1}}{3{t}^{2}+4}$.
∴${S}_{△A{F}_{1}B}$=$\frac{1}{2}|{F}_{1}{F}_{2}|$•|y1-y2|=$\frac{1}{2}×2c$×$\frac{12c\sqrt{{t}^{2}+1}}{3{t}^{2}+4}$=$\frac{12{c}^{2}\sqrt{{t}^{2}+1}}{3{t}^{2}+4}$.
设$\sqrt{{t}^{2}+1}$=m≥1,则t2=m2-1,∴${S}_{△A{F}_{1}B}$=$\frac{12{c}^{2}m}{3{m}^{2}+1}$=$\frac{12{c}^{2}}{3m+\frac{1}{m}}$,
令f(m)=3m+$\frac{1}{m}$,则f′(m)=3-$\frac{1}{{m}^{2}}$>0,
∴函数f(m)在[1,+∞)上单调递增,因此m=1,t=0时,△F1AB的面积取得最大值3c2.
设△F1AB的内切圆的半径为r,则${S}_{△A{F}_{1}B}$=$\frac{1}{2}r×4a$=4cr≤3c2.
∴r≤$\frac{3c}{4}$,
∴$π×(\frac{3c}{4})^{2}$=$\frac{9π}{16}$,解得c=1.
∴椭圆的方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1.
点评 本题考查了椭圆的标准方程及其性质、正三角形的性质、直线与椭圆相交弦长问题、一元二次方程的根与系数的关系、利用导数研究函数的单调性极值与最值、三角形的内切圆的性质与面积,考查了推理能力与计算能力,属于难题.


 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a3+a7≥b2+b6 | B. | a3+a7≤b2+b6 | ||
| C. | a3+a7≠b2+b6 | D. | a3+a7与b2+b6 大小不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
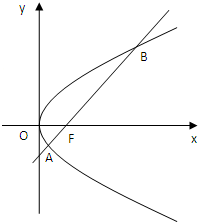 如图,斜率为1的直线过抛物线y2=2px(p>0)的焦点,与抛物线交于两点A.B,将直线AB向左平移p个单位得到直线l,N为l上的动点.
如图,斜率为1的直线过抛物线y2=2px(p>0)的焦点,与抛物线交于两点A.B,将直线AB向左平移p个单位得到直线l,N为l上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com