
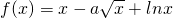 (a为常数).
(a为常数).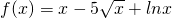 ,∴
,∴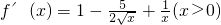 ,=
,=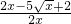 =
=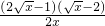
| x | 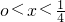 | 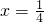 | 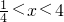 | x=4 | x>4 | |
| f′(x) | + | 0 | - | 0 | + | |
| f(x) | 递增 | 极大值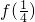 | 递减 | 极小值f(4) | 递增 |
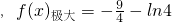 ,f(x)极小=-6+ln4
,f(x)极小=-6+ln4 …(8分)∴
…(8分)∴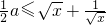
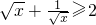 (当且仅当x=1时,
(当且仅当x=1时,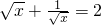 )∴
)∴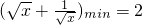 …(13分)∴a∈(-∞,4]
…(13分)∴a∈(-∞,4]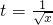 ,则:
,则: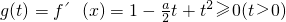
 或
或 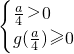
 看做一个整体,用t表示,则f'(x)可看做关于t的二次函数,即关于t的二次函数图象恒在x轴上方,在判断参数a份额范围.
看做一个整体,用t表示,则f'(x)可看做关于t的二次函数,即关于t的二次函数图象恒在x轴上方,在判断参数a份额范围.

科目:高中数学 来源:2012年宁夏高考数学仿真模拟试卷3(文科)(解析版) 题型:解答题
 ( a为常数、a∈R),
( a为常数、a∈R), .
.查看答案和解析>>
科目:高中数学 来源:2010年上海市普陀区曹杨二中高考数学模拟试卷(文科)(解析版) 题型:解答题
 (a为常数)的图象经过点(1,3).
(a为常数)的图象经过点(1,3).查看答案和解析>>
科目:高中数学 来源:2009-2010学年安徽省皖中地区示范高中高三联考数学试卷(文科)(解析版) 题型:解答题
 ( a为常数、a∈R),
( a为常数、a∈R), .
.查看答案和解析>>
科目:高中数学 来源:2010年青海省高一上学期期中考试数学试卷 题型:解答题
已知函数 (a为常数)是R上的奇函数,函数
(a为常数)是R上的奇函数,函数
是区间[-1,1]上的减函数.
(1)求a的值;
(2)若 上恒成立,求t的取值范围
上恒成立,求t的取值范围
查看答案和解析>>
科目:高中数学 来源:2010年贵州省遵义市高三考前最后一次模拟测试数学(理)试题 题型:解答题
(本小题满分12分)
已知函数 其中a为常数,且
其中a为常数,且 .
.
(Ⅰ)当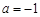 时,求
时,求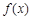 在
在 (e=2.718 28…)上的值域;
(e=2.718 28…)上的值域;
(Ⅱ)若 对任意
对任意 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com