练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

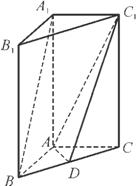
    如图,在直三棱柱A1B1C1-ABC中,AB⊥AC,AB=AC=2,A1A=4,点D是BC的中点.

    (1) 求异面直线A1B与C1D所成角的余弦值;

    (2) 求平面ADC1与平面ABA1所成二面角的平面角的正弦值.


     (1) 　(2)


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


     某校心理学研究小组在对学生上课注意力集中情况的调查研究中,发现其注意力指数p与听课时间t之间的关系满足如图所示的曲线.当t∈(0,14]时,曲线是二次函数图象的一部分;当t∈[14,40]时,曲线是函数y=loga(x-5)+83(a>0且a≠1)图象的一部分.根据专家研究,当注意力指数p≥80时,听课效果最佳.

    (1) 试求p=f(t)的函数关系式;

    (2) 教师在什么时段内安排核心内容,能使得学生听课效果最佳?请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}是等差数列,且a1,a2,a3是的展开式的前三项的系数,求的展开式的中间项.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     已知一圆柱的侧面展开图是长和宽分别为3π和π的矩形,则该圆柱的体积是　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知矩形ABCD和矩形ADEF所在平面互相垂直,点M,N分别在对角线BD,AE上,且BM=BD,AN=AE.求证:MN∥平面CDE.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图,在四棱锥P-ABCD中,PA⊥底面ABCD,BC=CD=2,AC=4,∠ACB=∠ACD=,点F为PC的中点,AF⊥PB,求PA的长.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知矩阵M=,点A(1,0)在矩阵M对应变换作用下变为A'(1,2),求矩阵M的逆矩阵M-1.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图,已知椭圆C1的中心在原点O,长轴的左、右端点M,N在x轴上,椭圆C2的短轴为MN,且椭圆C1,C2的离心率都为e,直线l⊥MN,l与椭圆C1交于B,C两点,与椭圆C2交于A,D两点,这四点按纵坐标从大到小依次为A,B,C,D.

    (1) 设e=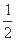,求BC与AD的比值;

    (2) 当e变化时,是否存在直线l,使得|BO∥AN|请说明理由.

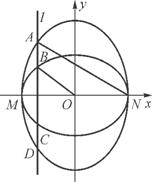
    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(x)=2sin,x∈的单调增区间为　　　　. 

    查看答案和解析>>

    同步练习册答案