练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．若函数f（x）=a-x（a＞0且a≠1）在（-∞，+∞）上是减函数，则g（x）=loga（x-1）的大致图象是（　　）
    A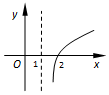．B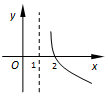．C．D．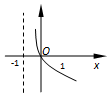

    分析 函数f（x）=a-x=$（\frac{1}{a}）^{x}$（a＞0且a≠1）在（-∞，+∞）上是减函数，可得$0＜\frac{1}{a}＜1$，a＞1．则g（x）=loga（x-1）的定义域为{x|x＞1}，在定义域内单调递增，且g（2）=0．即可得出．

    解答 解：∵函数f（x）=a-x=$（\frac{1}{a}）^{x}$（a＞0且a≠1）在（-∞，+∞）上是减函数，∴$0＜\frac{1}{a}＜1$，∴a＞1．
    则g（x）=loga（x-1）的定义域为{x|x＞1}，在定义域内单调递增，且g（2）=0．
    其大致图象是A．
    故选：A．

    点评 本题考查了指数函数的定义域与单调性、图象与性质，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    8．某药厂在动物体内进行新药试验，已知每投放剂量为m（m＞0）的药剂后，经过x小时该药剂在动物体内释放的浓度y（y毫克/升）满足函数y=mf（x），其中f（x）=$\left\{\begin{array}{l}-\frac{1}{2}{x^2}+2x+8，0＜x≤4\\-\frac{x}{2}-{log_2}x+12，4＜x≤16\end{array}$当药剂在动物体内释放的浓度不低于12（毫克/升）时，称为该药剂达到有效．
    （1）为了使在8小时之内（从投放药剂算起包括8小时）始终有效，求应该投放的药剂m的最小值；
    （2）若m=2，k 为整数，若该药在k 小时之内始终有效，求k的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

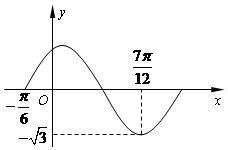    9．设函数f（x）=Asin（ωx+φ）（A，ω，φ为常数，且A＞0，ω＞0，0＜φ＜π）的部分图象如图所示．
    （1）求A，ω，φ的值；
    （2）设θ为锐角，且f（θ）=-$\frac{3}{5}\sqrt{3}$，求f（θ-$\frac{π}{6}$）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．求双曲线C：$\frac{x^2}{8}$-$\frac{y^2}{12}$=1的焦点坐标、实轴长、虚轴长及渐近线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知函数f（x）=kx2-lnx，若f（x）＞0在函数定义域内恒成立，则k的取值范围是（　　）
    A．$（{\frac{1}{e}，e}）$B．$（{\frac{1}{2e}，\frac{1}{e}}）$C．$（{-∞，\frac{1}{2e}}）$D．$（{\frac{1}{2e}，+∞}）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．下列各组函数中不表示同一函数的是（　　）
    A．f（x）=lgx2，g（x）=2lg|x|B．f（x）=x，g（x）=$\root{3}{{x}^{3}}$
    C．f（x）=$\sqrt{{x}^{2}-4}$，g（x）=$\sqrt{x+2}$$•\sqrt{x-2}$D．f（x）=|x+1|，g（x）=$\left\{\begin{array}{l}{x+1，x≥-1}\\{-x-1，x＜-1}\end{array}\right.$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．函数f（x）=$\sqrt{x+3}$+$\frac{1}{x+2}$的定义域为（　　）
    A．{x|x≥-3且x≠-2}B．{x|x≥-3且x≠2}C．{x|x≥-3}D．{x|x≥-2且x≠3}

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．设双曲线C：$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1（a＞0，b＞0）左，右焦点为F1，F2，P是双曲线C上的一点，PF1与x轴垂直，△PF1F2的内切圆方程为（x+1）2+（y-1）2=1，则双曲线方程为（　　）
    A．$\frac{x^2}{2}-\frac{y^2}{3}=1$B．${x^2}-\frac{y^2}{2}=1$C．$\frac{x^2}{2}-{y^2}=1$D．${x^2}-\frac{y^2}{3}=1$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．在平面直角坐标系中，不等式组$\left\{\begin{array}{l}{x+2y≥0}\\{2x-y≥0（a＞0）}\\{x≤a}\end{array}\right.$表示的平面区域的面积为5，则a=2．

    查看答案和解析>>

    同步练习册答案