
���� ��1����������Ľ���ʽ�����ݺ����ĵ����Կɵù���m�IJ���ʽ�飬��ü������m�ķ�Χ��������Խ������
��2����m=2���õ�y=2f��x�������ݺ����Ķ�����ֶ����ۼ��������
��� �⣺��1����$y=mf��x��=\left\{\begin{array}{l}-\frac{m}{2}{��x-2��^2}+10m��0��x��4\\-\frac{mx}{2}-m{log_2}x+12m��4��x��16\end{array}\right.$��
��֪�����䣨0��4]���У���8m��y��10m��
��f��x�������䣨4��16]�ϵ����ݼ���mf��8��=5m��
Ϊʹy��12�������ֻҪ$\left\{{\begin{array}{l}{8m��12}\\{5m��12}\end{array}}\right.$��
��$m��\frac{12}{5}$���ɵ�$m��\frac{12}{5}$��
����Ϊ��ʹ��8Сʱ֮�ڴﵽ��Ч��Ͷ�ŵ�ҩ������m����СֵΪ$\frac{12}{5}$��
��2��m=2ʱ����$y=g��x��=\left\{\begin{array}{l}-{x^2}+4x+16��0��x��4\\-x-2{log_2}x+24��4��x��16\end{array}\right.$
��0��x��4ʱ��16��-x2+4x+16��20����Ȼ�������⣬
��f��x�������䣨4��16]�ϵ����ݼ���
��g��6��=18-2log26=18-log236��12��
g��7��=17-2log27=17-log249��12��
�ɵ� k��6����k�����ֵΪ6��
���� ���⿼�麯�������������е�ʵ��Ӧ�ã�����ʱҪ�������⣬��ϸ��������������ϵ�������ؽ��еȼ�ת����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {a��e} | B�� | {c} | C�� | {d��f} | D�� | {b��c��d��f} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
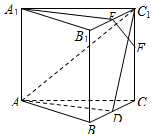 ��ͼ������������ABC-A1B1C1�У���֪D��E�ֱ�ΪBC��B1C1���е㣬��F����CC1�ϣ���EF��C1D����֤��
��ͼ������������ABC-A1B1C1�У���֪D��E�ֱ�ΪBC��B1C1���е㣬��F����CC1�ϣ���EF��C1D����֤���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 3 | C�� | log23 | D�� | log32 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 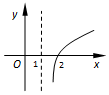 | B�� | 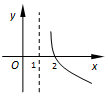 | C�� |  | D�� | 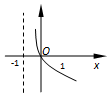 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com