
【题目】一款击鼓小游戏的规则如下:每盘游戏都需击鼓三次,每次击鼓要么出现一次音乐,要么不出现音乐;每盘游戏击鼓三次后,出现一次音乐获得10分,出现两次音乐获得20分,出现三次音乐获得100分,没有出现音乐则扣除200分(即获得-200分).设每次击鼓出现音乐的概率为![]() ,且各次击鼓出现音乐相互独立.
,且各次击鼓出现音乐相互独立.
(1)设每盘游戏获得的分数为X,求X的分布列;
(2)玩三盘游戏,至少有一盘出现音乐的概率为多少?
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() .
.
(1)若![]() 在
在![]() 处有极值,问是否存在实数m,使得不等式
处有极值,问是否存在实数m,使得不等式![]() 对任意
对任意![]() 及
及![]() 恒成立?若存在,求出m的取值范围;若不存在,请说明理由.
恒成立?若存在,求出m的取值范围;若不存在,请说明理由.![]() ;
;
(2)若![]() ,设
,设![]() .
.
①求证:当![]() 时,
时,![]() ;
;
②设![]() ,求证:
,求证:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC-A1B1C1中,底面△ABC是直角三角形,AC=BC=AA1=2,D为侧棱AA1的中点.

(1)求异面直线DC1,B1C所成角的余弦值;
(2)求二面角B1-DC-C1的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点A(0,﹣2),B(4,0),圆C经过点(0,﹣1),(0,1)及(![]() ,0).斜率为k的直线l经过点B.
,0).斜率为k的直线l经过点B.
(1)求圆C的标准方程;
(2)当k=2时,过直线l上的一点P向圆C引一条切线,切点为Q,且满足PQ=![]() ,求点P的坐标;
,求点P的坐标;
(3)设M,N是圆C上任意两个不同的点,若以MN为直径的圆与直线l都没有公共点,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校书法兴趣组有3名男同学A,B,C和3名女同学X,Y,Z,其年级情况如下表:
一年级 | 二年级 | 三年级 | |
男同学 | A | B | C |
女同学 | X | Y | Z |
现从这6名同学中随机选出2人参加书法比赛![]() 每人被选到的可能性相同
每人被选到的可能性相同![]() .
.
![]() 用表中字母列举出所有可能的结果;
用表中字母列举出所有可能的结果;
![]() 设M为事件“选出的2人来自不同年级且性别相同”,求事件M发生的概率.
设M为事件“选出的2人来自不同年级且性别相同”,求事件M发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.
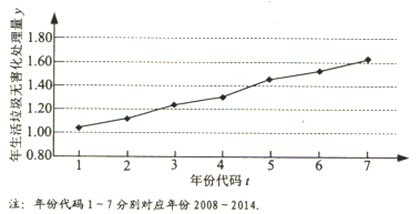
(Ⅰ)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;
(Ⅱ)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
附注:
参考数据:![]() ,
,![]() ,
,
![]() ,
,![]() ≈2.646.
≈2.646.
参考公式:相关系数
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司培训员工某项技能,培训有如下两种方式:
方式一:周一到周五每天培训1小时,周日测试
方式二:周六一天培训4小时,周日测试
公司有多个班组,每个班组60人,现任选两组![]() 记为甲组、乙组
记为甲组、乙组![]() 先培训;甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如表:
先培训;甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如表:
第一周 | 第二周 | 第三周 | 第四周 | |
甲组 | 20 | 25 | 10 | 5 |
乙组 | 8 | 16 | 20 | 16 |
![]() 用方式一与方式二进行培训,分别估计员工受训的平均时间
用方式一与方式二进行培训,分别估计员工受训的平均时间![]() 精确到
精确到![]() ,并据此判断哪种培训方式效率更高?
,并据此判断哪种培训方式效率更高?
![]() 在甲乙两组中,从第三周培训后达标的员工中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人中至少有1人来自甲组的概率.
在甲乙两组中,从第三周培训后达标的员工中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人中至少有1人来自甲组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,直线
,直线![]() 与函数
与函数![]() 的图象在
的图象在![]() 处相切,设
处相切,设![]() ,若在区间[1,2]上,不等式
,若在区间[1,2]上,不等式![]() 恒成立.则实数m( )
恒成立.则实数m( )
A. 有最大值![]() B. 有最大值e C. 有最小值e D. 有最小值
B. 有最大值e C. 有最小值e D. 有最小值![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com