
分析 根据已知条件,作出图形,MN的中点连接椭圆的两个焦点,便会得到三角形的中位线,根据中位线的性质及椭圆上的点到两焦点的距离和为2a即可求出|AN|+|BN|.
解答 解:椭圆C:$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1,a=5,b=4,c=3
设MN的中点为Q,椭圆C的左右焦点分别为F1,F2,
如图,连接QF1,QF2,
∵F1是MA的中点,Q是MN的中点,
∴F1Q是△MAN的中位线;
丨QF1丨=$\frac{1}{2}$丨AN丨,
同理:丨QF2丨=$\frac{1}{2}$丨NB丨,
∵Q在椭圆C上,
∴|QF1|+|QF2|=2a=10,
∴|AN|+|BN|=2(|QF1|+|QF2|)=20.
故答案为20.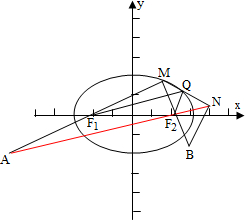
点评 本题考查椭圆的定义,椭圆的基本性质的应用,三角形的中位线定理,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,α∥β,则m∥β | B. | 若α⊥β,m?α,则m⊥β | ||
| C. | 若m⊥α,m∥n,α⊥β,则n∥β | D. | 若m⊥α,m∥n,α∥β,则n⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于x轴对称 | B. | 关于y轴对称 | C. | 关于y=x轴对称 | D. | 关于原点轴对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
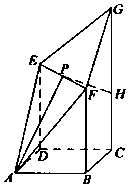 如图,四边形ABCD是边长为$\sqrt{2}$的正方形,CG⊥平面ABCD,DE∥BF∥CG,DE=BF=$\frac{3}{5}$CG.P为线段EF的中点,AP与平面ABCD所成角为60°.在线段CG上取一点H,使得GH=$\frac{3}{5}$CG.
如图,四边形ABCD是边长为$\sqrt{2}$的正方形,CG⊥平面ABCD,DE∥BF∥CG,DE=BF=$\frac{3}{5}$CG.P为线段EF的中点,AP与平面ABCD所成角为60°.在线段CG上取一点H,使得GH=$\frac{3}{5}$CG.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 9 | C. | 27 | D. | 81 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在几何体A1B1D1-ABCD中,四边形A1B1BA与A1D1DA均为直角梯形,且AA1⊥底面ABCD,四边形ABCD为正方形,AB=2A1D1=2A1B1=4,AA1=4,P为DD1的中点.
如图,在几何体A1B1D1-ABCD中,四边形A1B1BA与A1D1DA均为直角梯形,且AA1⊥底面ABCD,四边形ABCD为正方形,AB=2A1D1=2A1B1=4,AA1=4,P为DD1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com