
分析 (Ⅰ)根据频率分布直方图求出m的值;(Ⅱ)根据条件概率求出两组中各有一户被选中的概率即可.
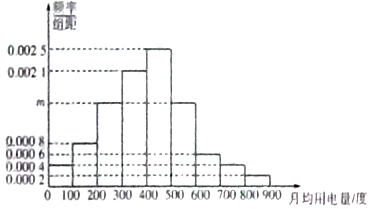
解答 解:(Ⅰ)1-100×(0.0004+0.0008+0.0021+0.0025+0.0006+0.0004+0.0002)=2m×100,
∴m=0.0015.
设中位数是x度,前5组的频率之和为0.04+0.08+0.15+0.21+0.25=0.73>0.5,
而前4组的频率之和为0.04+0.08+0.15+0.21=0.48<0.5,
所以400<x<500,$x-400=\frac{0.5-0.48}{0.25}×100$,
故x=408,即居民月均用电量的中位数为408度.
(Ⅱ)第8组的户数为0.0004×100×100=4,分别设为A1,A2,A3,A4,
第9组的户数为0.0002×100×100=2,分别设为B1,B2,
则从中任选出2户的基本事件为:
(A1,A2),(A1,A3),(A1,A4),(A1,B1),(A1,B2),
(A2,A3),(A2,A4),(A2,B1),(A2,B2),(A3,A4),
(A3,B1),(A3,B2),(A4,B1),(A4,B2),(B1,B2)共15种.
其中两组中各有一户被选中的基本事件为:
(A1,B1),(A1,B2),(A2,B1),(A2,B2),
(A3,B1),(A3,B2),(A4,B1),(A4,B2)共8种.
所以第8,9组各有一户被选中的概率$P=\frac{8}{15}$.
点评 本题考查了频率分布直方图问题,考查条件概率问题,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄段 | 18-24岁 | 25-49岁 | 50-64岁 | 65岁及以上 |
| 频数 | 35 | 20 | 25 | 20 |
| 支持脱欧的人数 | 10 | 10 | 15 | 15 |
| 年龄低于50岁的人数 | 年龄不低于50岁的人数 | 合计 | |
| 支持“脱欧”人数 | |||
| 不支持“脱欧”人数 | |||
| 合计 |
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| K0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 0或-1 | D. | 0或1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
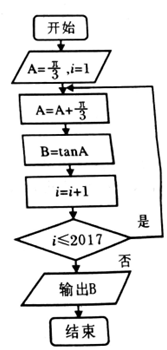
| A. | $\sqrt{3}$ | B. | 0 | C. | -$\frac{\sqrt{3}}{3}$ | D. | -$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com