
| 年龄段 | 18-24岁 | 25-49岁 | 50-64岁 | 65岁及以上 |
| 频数 | 35 | 20 | 25 | 20 |
| 支持脱欧的人数 | 10 | 10 | 15 | 15 |
| 年龄低于50岁的人数 | 年龄不低于50岁的人数 | 合计 | |
| 支持“脱欧”人数 | |||
| 不支持“脱欧”人数 | |||
| 合计 |
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| K0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
分析 (Ⅰ)根据统计数据,可得2×2列联表,根据列联表中的数据,计算K2的值,即可得到结论;
(Ⅱ)利用列举法确定基本事件的个数,即可得出这2人至少有1人年龄在18-24岁的概率.
解答 解:(Ⅰ)
| 年龄低于50岁的人数 | 年龄不低于50岁的人数 | 合计 | |
| 支持“脱欧”人数 | 20 | 30 | 50 |
| 不支持“脱欧”人数 | 35 | 15 | 50 |
| 合计 | 55 | 45 | 100 |
点评 本题考查独立性检验,考查概率的计算,考查学生的阅读与计算能力,属于中档题.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
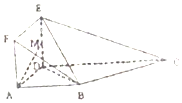 如图,在多面体ABCDEF中,平面ADEF与平面ABCD垂直,ADEF是正方形,在直角梯形ABCD中,AB∥CD,AB⊥AD,且AB=AD=$\frac{1}{2}$CD=1,M为线段ED的中点.
如图,在多面体ABCDEF中,平面ADEF与平面ABCD垂直,ADEF是正方形,在直角梯形ABCD中,AB∥CD,AB⊥AD,且AB=AD=$\frac{1}{2}$CD=1,M为线段ED的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com