
分析 设E,E1分别是BC,B1C1的中点,O,O1分别是下、上底面正方形的中心,则O1O是正四棱台的高,且O1O=12,连结OE,O1E1,则OE=6,O1E1=3,过E1作E1H⊥OE,垂足为H,则E1H=O1O=12,OH=O1E1=3,HE=3,${E}_{1}E=3\sqrt{17}$,由此能求出该正四棱台的侧面积、体积.
解答 解: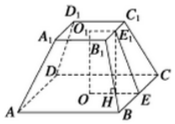 如图,E,E1分别是BC,B1C1的中点,O,O1分别是下、上底面正方形的中心,
如图,E,E1分别是BC,B1C1的中点,O,O1分别是下、上底面正方形的中心,
则O1O是正四棱台的高,则O1O=12,
连结OE,O1E1,则OE=$\frac{1}{2}$AB=$\frac{1}{2}×12$=6,O1E1=$\frac{1}{2}$A1B1=3,
过E1作E1H⊥OE,垂足为H,
则E1H=O1O=12,OH=O1E1=3,HE=OE-O1E1=6-3=3,
在Rt△E1HE中,E1E2=E1H2+HE2=122+32=32×42+32=32×17,
∴${E}_{1}E=3\sqrt{17}$,
∴该正四棱台的侧面积为
${S}_{侧}=4×\frac{1}{2}×({B}_{1}{C}_{1}+BC)×{E}_{1}E$=$2×(12+6)×3\sqrt{17}=108\sqrt{17}$.
S上=62=36,S下=122=144,h=12,
∴该正四棱台的体积为:
V=$\frac{h}{3}({S}_{上}+{S}_{下}+\sqrt{{S}_{上}{S}_{下}})$=$\frac{12}{3}(36+144+\sqrt{36×144})$=1008.
点评 本题主要考查正四棱台的侧面积和体积的求法,考查直线与直线、直线与平面、平面与平面的位置关系及体积计算等基础知识;考查学生的空间想象能力、推理论证能力及运算求解能力;考查了化归与转化及数形结合的数学思想.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
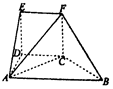 如图,几何体EF-ABCD中,DE⊥平面ABCD,CDEF是正方形,ABCD为直角梯形,AB∥CD,AD⊥DC,△ACB的腰长为$2\sqrt{2}$的等腰直角三角形.
如图,几何体EF-ABCD中,DE⊥平面ABCD,CDEF是正方形,ABCD为直角梯形,AB∥CD,AD⊥DC,△ACB的腰长为$2\sqrt{2}$的等腰直角三角形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:甲商场:顾客转动如图所示圆盘,当指针指向阴影部分(图中两个阴影部分均为扇形,且每个扇形圆心角均为$\frac{π}{4}$,边界忽略不计)即为中奖.乙商场:从装有2个白球、2个蓝球和2个红球的盒子中一次性摸出1球(这些球除颜色外完全相同),它是红球的概率是$\frac{1}{3}$,若从盒子中一次性摸出2球,且摸到的是2个相同颜色的球,即为中奖.
甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:甲商场:顾客转动如图所示圆盘,当指针指向阴影部分(图中两个阴影部分均为扇形,且每个扇形圆心角均为$\frac{π}{4}$,边界忽略不计)即为中奖.乙商场:从装有2个白球、2个蓝球和2个红球的盒子中一次性摸出1球(这些球除颜色外完全相同),它是红球的概率是$\frac{1}{3}$,若从盒子中一次性摸出2球,且摸到的是2个相同颜色的球,即为中奖.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知平行四边形ABCD的三个顶点的坐标为A(-1,4),B(-2,-1),C(2,3).
如图,已知平行四边形ABCD的三个顶点的坐标为A(-1,4),B(-2,-1),C(2,3).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄段 | 18-24岁 | 25-49岁 | 50-64岁 | 65岁及以上 |
| 频数 | 35 | 20 | 25 | 20 |
| 支持脱欧的人数 | 10 | 10 | 15 | 15 |
| 年龄低于50岁的人数 | 年龄不低于50岁的人数 | 合计 | |
| 支持“脱欧”人数 | |||
| 不支持“脱欧”人数 | |||
| 合计 |
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| K0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com