
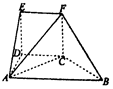
 如图,几何体EF-ABCD中,DE⊥平面ABCD,CDEF是正方形,ABCD为直角梯形,AB∥CD,AD⊥DC,△ACB的腰长为$2\sqrt{2}$的等腰直角三角形.
如图,几何体EF-ABCD中,DE⊥平面ABCD,CDEF是正方形,ABCD为直角梯形,AB∥CD,AD⊥DC,△ACB的腰长为$2\sqrt{2}$的等腰直角三角形.分析 (I)证明AC⊥BC.DE⊥BC.得到CF⊥BC.即可证明BC⊥平面ACF.推出BC⊥AF.
(Ⅱ)以点D为原点,DA,DC,DE分别为x,y,z轴建立空间直角坐标系,求出平面ABF的法向量,平面ACF的一个法向量,设二面角B-AF-C的大小为θ,利用空间向量的数量积求解即可.
解答 (I)证明:因为△ACB是腰长为$2\sqrt{2}$的等腰直角三角形,所以AC⊥BC.
因为DE⊥平面ABCD,所以DE⊥BC.
又DE∥CF,所以CF⊥BC.
又AC∩CF=C,所以BC⊥平面ACF.
所以BC⊥AF.
(Ⅱ)解:以点D为原点,DA,DC,DE分别为x,y,z轴建立如下图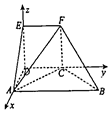
所示的空间直角坐标系:
因为△ACB是腰长为$2\sqrt{2}$的等腰直角三角形,
所以$AC=BC=2\sqrt{2}$,$AB=\sqrt{A{C^2}+B{C^2}}=4$.
所以$AD=BCsin∠ABC=2\sqrt{2}×sin{45°}=2$,$CD=AB-BCcos∠ABC=4-2\sqrt{2}×cos{45°}=2$.
所以DE=EF=CF=2.
则点A(2,0,0),F(0,2,2),C(0,2,0),B(2,4,0).
则$\overrightarrow{AB}=(0,4,0),\overrightarrow{AF}=(-2,2,2)$.
设平面ABF的法向量为$\vec m=(x,y,z)$,则
由$\left\{\begin{array}{l}\vec m•\overrightarrow{AB}=0\\ \vec m•\overrightarrow{AF}=0\end{array}\right.$得$\left\{\begin{array}{l}(x,y,z)•(0,4,0)=0\\(x,y,z)•(-2,2,2)=0\end{array}\right.$得$\left\{\begin{array}{l}4y=0\\-2x+2y+2z=0\end{array}\right.$得$\left\{\begin{array}{l}y=0\\ z=x\end{array}\right.$
令x=1,得$\vec m=(1,0,1)$是平面ABF的一个法向量;
易知平面ACF的一个法向量$\overrightarrow{CB}=(2,2,0)$;
设二面角B-AF-C的大小为θ,则$cosθ=|{cos(\vec m,\overrightarrow{CB})}|=|{\frac{{\vec m•\overrightarrow{CB}}}{{|{\vec m}||{\overrightarrow{CB}}|}}}|=|{\frac{(1,0,1)•(2,2,0)}{{\sqrt{2}×2\sqrt{2}}}}|=\frac{1}{2}$,
又θ∈(0°,180°),解得θ=60°.
故二面角B-AF-C的大小为60°.
点评 本题考查空间向量的数量积的应用,二面角的平面角的求法,直线与平面垂直的判定定理的应用,考查计算能力.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点P(2,$\sqrt{2}$),离心率e=$\frac{\sqrt{2}}{2}$,直线l的渐近线为x=4.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点P(2,$\sqrt{2}$),离心率e=$\frac{\sqrt{2}}{2}$,直线l的渐近线为x=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $\frac{3}{4}$ | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
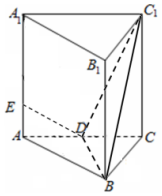 已知正三棱柱ABC-A1B1C1中,AB=AA1=2,点D为AC的中点,点E为AA1上.
已知正三棱柱ABC-A1B1C1中,AB=AA1=2,点D为AC的中点,点E为AA1上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,α∥β,则m∥β | B. | 若α⊥β,m?α,则m⊥β | ||
| C. | 若m⊥α,m∥n,α⊥β,则n∥β | D. | 若m⊥α,m∥n,α∥β,则n⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com