
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点P(2,$\sqrt{2}$),离心率e=$\frac{\sqrt{2}}{2}$,直线l的渐近线为x=4.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点P(2,$\sqrt{2}$),离心率e=$\frac{\sqrt{2}}{2}$,直线l的渐近线为x=4.分析 (1)利用点$P(2,\sqrt{2})$在椭圆上,椭圆的离心率,求解a,b,得到椭圆方程.
(2)假设存在常数λ,使得k1+k2=λk3.设AB的斜率为k,则直线AB的方程为y=k(x-2),代入椭圆方程,设A(x1,y1),B(x2,y2),利用韦达定理,结合A、F、B共线,通过k=kAF=kBF,求出k1+k2,然后推出k1+k2=2k3.即可.
解答 解:(1)由点$P(2,\sqrt{2})$在椭圆上得,$\frac{4}{a^2}+\frac{2}{b^2}=1$①$又e=\frac{{\sqrt{2}}}{2},所以\frac{c}{a}=\frac{{\sqrt{2}}}{2}$②
由 ①②得c2=4,a2=8,b2=4,故椭圆C的方程为$\frac{x^2}{8}+\frac{y^2}{4}=1$…..(4分)
(2)假设存在常数λ,使得k1+k2=λk3.
由题意可设AB的斜率为k,则直线AB的方程为y=k(x-2)③
代入椭圆方程$\frac{x^2}{8}+\frac{y^2}{4}=1$并整理得(1+2k2)x2-8k2x+8k2-8=0
设A(x1,y1),B(x2,y2),则有${x_1}+{x_2}=\frac{{8{k^2}}}{{1+2{k^2}}},{x_1}{x_2}=\frac{{8{k^2}-8}}{{1+2{k^2}}}$④…(6分)
在方程③中,令x=4得,M(4,2k),从而${k}_{1}=\frac{{y}_{1}-\sqrt{2}}{{x}_{1}-2}$,${k}_{2}=\frac{{y}_{2}-\sqrt{2}}{{x}_{2}-2}$,${k_3}=\frac{{2k-\sqrt{2}}}{4-2}=k-\frac{{\sqrt{2}}}{2}$.
又因为A、F、B共线,则有k=kAF=kBF,
即有$\frac{y_1}{{{x_1}-2}}=\frac{y_2}{{{x_2}-2}}=k$…(8分)
所以k1+k2=$\frac{{{y_1}-\sqrt{2}}}{{{x_1}-2}}+\frac{{{y_2}-\sqrt{2}}}{{{x_2}-2}}$=$\frac{y_1}{{{x_1}-2}}+\frac{y_2}{{{x_2}-2}}-\sqrt{2}(\frac{1}{{{x_1}-2}}+\frac{1}{{{x_2}-2}})$
=$2k-\sqrt{2}•$$\frac{{{x_1}+{x_2}-4}}{{{x_1}{x_2}-2({x_1}+{x_2})+4}}$⑤…(10分)
将④代入⑤得k1+k2=$2k-\sqrt{2}•$$\frac{{\frac{{8{k^2}}}{{1+2{k^2}}}-4}}{{\frac{{8{k^2}-8}}{{1+2{k^2}}}-2•\frac{{8{k^2}}}{{1+2{k^2}}}+4}}=2k-\sqrt{2}$,又${k_3}=k-\frac{{\sqrt{2}}}{2}$,
所以k1+k2=2k3.故存在常数λ=2符合题意…(12分)
点评 本题考查椭圆的方程的求法,直线与椭圆的位置关系的综合应用,考查转化思想以及计算能力.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:解答题
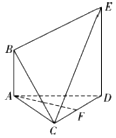 如图所示的多面体ABCDE中,已知AB∥DE,AB⊥AD,AD=2$\sqrt{3}$,AC=CD=DE=2AB=2,BC=$\sqrt{5}$,F是CD的中点.
如图所示的多面体ABCDE中,已知AB∥DE,AB⊥AD,AD=2$\sqrt{3}$,AC=CD=DE=2AB=2,BC=$\sqrt{5}$,F是CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知斜三棱柱ABC-A1B1C1的所有棱长均为2,∠B1BA=$\frac{π}{3}$,M,N分别为A1C1与B1C的中点,且侧面ABB1A1⊥底面ABC.
如图,已知斜三棱柱ABC-A1B1C1的所有棱长均为2,∠B1BA=$\frac{π}{3}$,M,N分别为A1C1与B1C的中点,且侧面ABB1A1⊥底面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
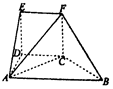 如图,几何体EF-ABCD中,DE⊥平面ABCD,CDEF是正方形,ABCD为直角梯形,AB∥CD,AD⊥DC,△ACB的腰长为$2\sqrt{2}$的等腰直角三角形.
如图,几何体EF-ABCD中,DE⊥平面ABCD,CDEF是正方形,ABCD为直角梯形,AB∥CD,AD⊥DC,△ACB的腰长为$2\sqrt{2}$的等腰直角三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com