
分析 (1)根据函数单调性定义法证明步骤:取值、作差、变形、定号、下结论,进行证明即可;
(2)由解析式求出定义域,化简f(-x)后由函数奇偶性的定义判断即可.
解答 证明:(1)任取1≤x1<x2,
则f(x2)-f(x1)=$\frac{2{x}_{2}}{{{x}_{2}}^{2}+1}$-$\frac{2{x}_{1}}{{{x}_{1}}^{2}+1}$
=$\frac{2{x}_{2}{{x}_{1}}^{2}+2{x}_{2}-2{x}_{1}{{x}_{2}}^{2}-2{x}_{1}}{{{({{x}_{1}}^{2}+1)(x}_{2}}^{2}+1)}$
=$\frac{2{x}_{1}{x}_{2}({x}_{1}-{x}_{2})+2({x}_{2}-{x}_{1})}{{({{x}_{1}}^{2}+1){(x}_{2}}^{2}+1)}$
=$\frac{2({x}_{2}-{x}_{1})(1-{x}_{1}{x}_{2})}{({{x}_{1}}^{2}+1){{(x}_{2}}^{2}+1)}$,
∵1≤x1<x2,∴x1x2>1,∴1-x1x2<0,
∴f(x2)<f(x1),∴f(x)在[1,+∞)上是减函数.
(2)∵f(x)的定义域为R,f(-x)=$\frac{2(-x)}{(-x)^{2}+1}$=$-\frac{2x}{{x}^{2}+1}$=-f(x),
∴f(x)为奇函数.
点评 本题考查函数单调性定义法证明步骤:取值、作差、变形、定号、下结论,以及函数奇偶性的判断方法:定义法,注意先求出函数的定义域,考查化简、变形能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
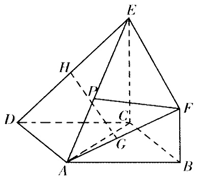 在如图所示的空间几何体中,EC⊥平面ABCD,四边形ABCD是菱形,CE∥BF,且CE=2BF,G,H,P分别为AF,DE,AE的中点.求证:
在如图所示的空间几何体中,EC⊥平面ABCD,四边形ABCD是菱形,CE∥BF,且CE=2BF,G,H,P分别为AF,DE,AE的中点.求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
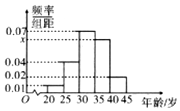 为创建全国文明城市,某区向各事业行政单位征集“文明过马路”义务督导员.从符合条件的600名志愿者中随机抽取100名,按年龄作分组如下:[20,25),[25,30),[30,35),[35,40),[40,45],并得到如下频率分布直方图.
为创建全国文明城市,某区向各事业行政单位征集“文明过马路”义务督导员.从符合条件的600名志愿者中随机抽取100名,按年龄作分组如下:[20,25),[25,30),[30,35),[35,40),[40,45],并得到如下频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点P(2,$\sqrt{2}$),离心率e=$\frac{\sqrt{2}}{2}$,直线l的渐近线为x=4.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点P(2,$\sqrt{2}$),离心率e=$\frac{\sqrt{2}}{2}$,直线l的渐近线为x=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,α∥β,则m∥β | B. | 若α⊥β,m?α,则m⊥β | ||
| C. | 若m⊥α,m∥n,α⊥β,则n∥β | D. | 若m⊥α,m∥n,α∥β,则n⊥β |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com