
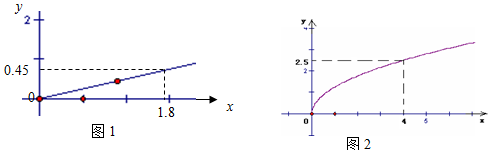
分析 (1)设投资为x万元,由题意,知f(1.8)=0.45,g(4)=2.5,由此能求出A、B两种产品的收益表示为投资的函数关系式.
(2)设对股票等风险型产品B投资x万元,则对债券等稳键型产品A投资(10-x)万元,记家庭进行理财投资获取的收益为y万元,则y=$\frac{1}{4}(10-x)+\frac{5}{4}\sqrt{x}$,x≥0.利用换元法能求出怎样分配这10万元投资,才能使投资获得最大收益,并能求出其最大收益为多少万元.
解答 解:(1)设投资为x万元,
由题意,知f(1.8)=0.45,g(4)=2.5;解得k1=$\frac{1}{4}$,k2=$\frac{5}{4}$,
∴f(x)=$\frac{1}{4}$x,x≥0.g(x)=$\frac{5}{4}\sqrt{x}$,x≥0;
(2)设对股票等风险型产品B投资x万元,则对债券等稳键型产品A投资(10-x)万元,
记家庭进行理财投资获取的收益为y万元,则y=$\frac{1}{4}(10-x)+\frac{5}{4}\sqrt{x}$,x≥0.
设$\sqrt{x}$=t,则x=t2,0≤t≤$\sqrt{10}$
∴y=-$\frac{1}{4}(t-\frac{5}{2})^{2}+$$\frac{65}{16}$,
当t=$\frac{5}{2}$,也即x=$\frac{25}{4}$时,y取最大值$\frac{65}{16}$.
答:对股票等风险型产品B投资$\frac{25}{4}$万元,对债券等稳键型产品A投资$\frac{15}{4}$万元时,可获最大收益$\frac{65}{16}$万元.
点评 本题的考点是函数模型的选择与应用,主要考查正比例函数模型,关键是将实际问题转化为数学问题.


科目:高中数学 来源: 题型:选择题
| A. | -x2-2sinx | B. | -x2+2sinx | C. | x2+2sinx | D. | x2-2sinx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
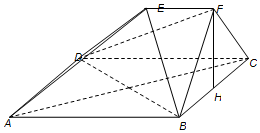 如图,在多面体ABCDEF中,四边形ABCD是正方形,AB=2EF=2,EF∥AB,EF⊥FB,∠BFC=90°,BF=FC,H为BC的中点,
如图,在多面体ABCDEF中,四边形ABCD是正方形,AB=2EF=2,EF∥AB,EF⊥FB,∠BFC=90°,BF=FC,H为BC的中点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
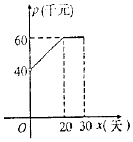 根据市场调查,某种新产品投放市场的30天内,每件的销售价格p(千元)与时间x(天)组成有序数对(x,p),点(x,p)落在下图中的两条线段上,且日销售量q(件)与时间x(天)之间的关系是q=-x+60(x∈N*).
根据市场调查,某种新产品投放市场的30天内,每件的销售价格p(千元)与时间x(天)组成有序数对(x,p),点(x,p)落在下图中的两条线段上,且日销售量q(件)与时间x(天)之间的关系是q=-x+60(x∈N*).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | $\frac{10}{3}$ | D. | $\frac{13}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com