
分析 (1)进行数量积的坐标运算得出f(x)=$2co{s}^{2}x+\sqrt{3}sin2x+a$,化简后即可得到$f(x)=2sin(2x+\frac{π}{6})+1+a$;
(2)由x的范围可得出2x+$\frac{π}{6}$的范围,从而求出f(x)的最大值2+1+a=2,求出a的值,并可写出f(x)的单调增减区间.
解答 解:(1)f(x)=$\overrightarrow{OA}•\overrightarrow{OB}$
=$2co{s}^{2}x+\sqrt{3}sin2x+a$
=$cos2x+\sqrt{3}sin2x+1+a$
=$2sin(2x+\frac{π}{6})+1+a$
(2)当x$∈[0,\frac{π}{2}]$时,2x+$\frac{π}{6}$$∈[\frac{π}{6},\frac{7π}{6}]$;
故f(x)max=2+1+a=2,解得a=-1;
f(x)的单调递增区间为$[-\frac{π}{3}+kπ,\frac{π}{6}+kπ]$,k∈Z;
单调递减区间为$[\frac{π}{6}+kπ,\frac{2π}{3}+kπ]$,k∈Z.
点评 考查向量数量积的坐标运算,二倍角的余弦公式,两角和的正弦公式,以及复合函数单调区间的求法.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
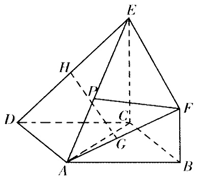 在如图所示的空间几何体中,EC⊥平面ABCD,四边形ABCD是菱形,CE∥BF,且CE=2BF,G,H,P分别为AF,DE,AE的中点.求证:
在如图所示的空间几何体中,EC⊥平面ABCD,四边形ABCD是菱形,CE∥BF,且CE=2BF,G,H,P分别为AF,DE,AE的中点.求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $\frac{3}{4}$ | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
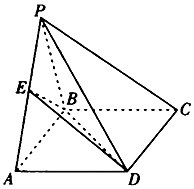 如图,四棱锥P-ABCD的底面ABCD是矩形,平面PAB⊥平面ABCD,E是PA的中点,且PA=PB=AB=4,$BC=\sqrt{2}$.
如图,四棱锥P-ABCD的底面ABCD是矩形,平面PAB⊥平面ABCD,E是PA的中点,且PA=PB=AB=4,$BC=\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
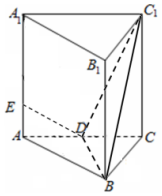 已知正三棱柱ABC-A1B1C1中,AB=AA1=2,点D为AC的中点,点E为AA1上.
已知正三棱柱ABC-A1B1C1中,AB=AA1=2,点D为AC的中点,点E为AA1上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,α∥β,则m∥β | B. | 若α⊥β,m?α,则m⊥β | ||
| C. | 若m⊥α,m∥n,α⊥β,则n∥β | D. | 若m⊥α,m∥n,α∥β,则n⊥β |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com