
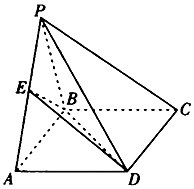
 如图,四棱锥P-ABCD的底面ABCD是矩形,平面PAB⊥平面ABCD,E是PA的中点,且PA=PB=AB=4,$BC=\sqrt{2}$.
如图,四棱锥P-ABCD的底面ABCD是矩形,平面PAB⊥平面ABCD,E是PA的中点,且PA=PB=AB=4,$BC=\sqrt{2}$.分析 (Ⅰ)连接AC,交BD于点O,连接EO,则PC∥EO,由此能证明PC∥平面EBD.
(Ⅱ)取AB中点H,连接PH,由V三棱锥A-PBD=V三棱锥P-ABD,能求出三棱锥A-PBD的体积.
解答 证明:(Ⅰ)连接AC,交BD于点O,连接EO,则O是AC的中点.
又∵E是PA的中点,∴EO是△PAC的中位线,∴PC∥EO,
又∵EO?平面EBD,PC?平面EBD,
∴PC∥平面EBD.
解:(Ⅱ)取AB中点H,连接PH,
由PA=PB得PH⊥AB,
又∵平面PAB⊥平面ABCD,
且平面PAB∩平面ABCD=AB,
∴PH⊥平面ABCD.
∵△PAB是边长为4的等边三角形,∴$PH=2\sqrt{3}$.
又∵${S_{△ABD}}=\frac{1}{2}×AB×AD$=$\frac{1}{2}×4×\sqrt{2}=2\sqrt{2}$,
∴V三棱锥A-PBD=V三棱锥P-ABD=$\frac{1}{3}{S_{△ABD}}•PH=\frac{1}{3}×2\sqrt{2}×2\sqrt{3}=\frac{{4\sqrt{6}}}{3}$.
点评 本题考查线面平行的证明,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 星级口算天天练系列答案
星级口算天天练系列答案科目:高中数学 来源: 题型:选择题
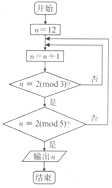 若正整数N除以正整数m后的余数为n,则记为N=n(modm),例如11=4(mod7),如图所示的程序框图的算法源于我国古代闻名中外的《中国剩余定理》,执行该程序框图,则输出的n=( )
若正整数N除以正整数m后的余数为n,则记为N=n(modm),例如11=4(mod7),如图所示的程序框图的算法源于我国古代闻名中外的《中国剩余定理》,执行该程序框图,则输出的n=( )| A. | 14 | B. | 15 | C. | 16 | D. | 17 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
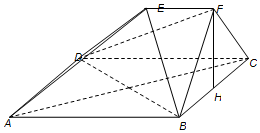 如图,在多面体ABCDEF中,四边形ABCD是正方形,AB=2EF=2,EF∥AB,EF⊥FB,∠BFC=90°,BF=FC,H为BC的中点,
如图,在多面体ABCDEF中,四边形ABCD是正方形,AB=2EF=2,EF∥AB,EF⊥FB,∠BFC=90°,BF=FC,H为BC的中点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | a=m,b=m | B. | b=m,a=m | C. | a=f(m),b=f(m) | D. | b=f(m),a=f(m) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
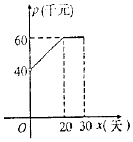 根据市场调查,某种新产品投放市场的30天内,每件的销售价格p(千元)与时间x(天)组成有序数对(x,p),点(x,p)落在下图中的两条线段上,且日销售量q(件)与时间x(天)之间的关系是q=-x+60(x∈N*).
根据市场调查,某种新产品投放市场的30天内,每件的销售价格p(千元)与时间x(天)组成有序数对(x,p),点(x,p)落在下图中的两条线段上,且日销售量q(件)与时间x(天)之间的关系是q=-x+60(x∈N*).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com