
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 利用辅助角公式将函数f(x)化简,结合三角函数的图象及性质依次对各项进行判断即可.
解答 解:函数$f(x)=\sqrt{3}{cos^2}x+2sinxcosx-\sqrt{3}{sin^2}x$,
化简可得:f(x)=$\sqrt{3}$cos2x+sin2x=2sin(2x+$\frac{π}{3}$),
对于①:当x=$\frac{π}{12}$时,函数f(x)取得最大值2,∴x=$\frac{π}{12}$是其中一条对称轴.故①对.
对于②:f(x+$\frac{π}{3}$)=2sin(2x+$\frac{π}{3}$+$\frac{2π}{3}$)=-2sin2x,
-f($\frac{π}{3}$-x)=-2sin(-2x+$\frac{π}{3}$+$\frac{2π}{3}$)=-2sin2x,
∴$?x∈R,f({\frac{π}{3}+x})=-f({\frac{π}{3}-x})$;故②对.
对于③将f(x)的图象向右平移$\frac{π}{3}$个单位,可得2sin[2(x$-\frac{π}{3}$)+$\frac{π}{3}$]=2sin(2x-$\frac{π}{3}$)不是奇函数,故③不对
④?x1,x2∈R,|f(x1)-f(x2)|≥4.
f(x)=2sin(2x+$\frac{π}{3}$),当x1=$\frac{π}{6}$,${x}_{2}=-\frac{5π}{12}$时,|f(x1)-f(x2)|=4,存在x1,x2∈R使得|f(x1)-f(x2)|≥4,故④对.
∴真命题的个数是3.
故选:C.
点评 本题主要考查三角函数的图象和性质,利用三角函数公式将函数进行化简是解决本题的关键.


科目:高中数学 来源: 题型:解答题
| 年龄段 | 18-24岁 | 25-49岁 | 50-64岁 | 65岁及以上 |
| 频数 | 35 | 20 | 25 | 20 |
| 支持脱欧的人数 | 10 | 10 | 15 | 15 |
| 年龄低于50岁的人数 | 年龄不低于50岁的人数 | 合计 | |
| 支持“脱欧”人数 | |||
| 不支持“脱欧”人数 | |||
| 合计 |
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| K0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
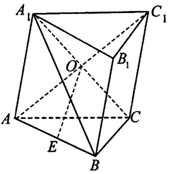 如图,在斜三梭柱ABC-A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,E是棱AB上一点,且OE∥平面BCC1B1
如图,在斜三梭柱ABC-A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,E是棱AB上一点,且OE∥平面BCC1B1查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 2 | 3 | 4 | 5 |
| y | 6.5 | m | n | 2.5 |
| A. | $\stackrel{∧}{y}$=0.8x+2.3 | B. | $\stackrel{∧}{y}$=2x+0.4 | C. | $\stackrel{∧}{y}$=-1.5x+8 | D. | $\stackrel{∧}{y}$=-1.6x+10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
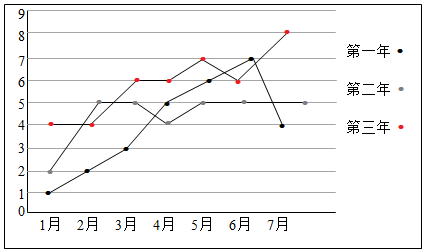
| 月份x | 1 | 2 | 3 | 4 |
| 利润y(单位:百万元) | 4 | 4 | 6 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | -3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com