
分析 (1)由于x=3是函数f(x)的一个极值点,可得f′(3)=0,解出并验证即可;
(2)求出函数g(x)的导数,通过讨论a的范围,得到函数g(x)的单调性,求出h(a)的解析式即可.
解答 解:(1)f′(x)=$\frac{a}{x}$+2x-a(x>0).
∵x=3是函数f(x)的一个极值点,
∴f′(3)=$\frac{a}{3}$+6-a=0,解得a=9,
∴f′(x)=$\frac{(2x-3)(x-3)}{x}$,
∴0<x<$\frac{3}{2}$或x>3时,f′(x)>0,$\frac{3}{2}$<x<3时,f′(x)<0,
∴x=3是函数f(x)的一个极小值点,
(2)g(x)=alnx+x2-ax-2x,x∈[1,e],
g′(x)=$\frac{(2x-a)(x-1)}{x}$,
①$\frac{a}{2}$≤1即a≤2时,g(x)在[1,e]递增,
g(x)min=g(1)=-a-1;
②1<$\frac{a}{2}$<2即2<a<2e时,
g(x)在[1,$\frac{a}{2}$)递减,在($\frac{a}{2}$,e]递增,
故g(x)min=g($\frac{a}{2}$)=aln$\frac{a}{2}$-$\frac{{a}^{2}}{4}$-a;
③$\frac{a}{2}$≥e即a≥2e时,g(x)在[1,e]递减,
故g(x)min=g(e)=a(1-e)+e(e-2);
综上h(a)=$\left\{\begin{array}{l}{-a-1,a≤2}\\{aln\frac{a}{2}-\frac{{a}^{2}}{4}-a,2<a<2e}\\{a(1-e)+e(e-2),a≥2e}\end{array}\right.$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
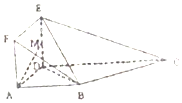 如图,在多面体ABCDEF中,平面ADEF与平面ABCD垂直,ADEF是正方形,在直角梯形ABCD中,AB∥CD,AB⊥AD,且AB=AD=$\frac{1}{2}$CD=1,M为线段ED的中点.
如图,在多面体ABCDEF中,平面ADEF与平面ABCD垂直,ADEF是正方形,在直角梯形ABCD中,AB∥CD,AB⊥AD,且AB=AD=$\frac{1}{2}$CD=1,M为线段ED的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
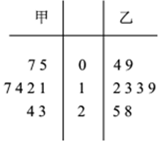 如图是甲、乙两个商场统计同一时间段各自每天的销售额(单位:万元)的茎叶图,假设销售额的中位数为m,平均值为$\overline{x}$,则下列正确的是( )
如图是甲、乙两个商场统计同一时间段各自每天的销售额(单位:万元)的茎叶图,假设销售额的中位数为m,平均值为$\overline{x}$,则下列正确的是( )| A. | m甲=m乙,$\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$ | B. | m甲=m乙,$\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$ | ||
| C. | m甲>m乙,$\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$ | D. | m甲<m乙,$\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
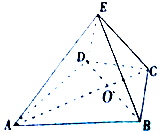 如图,在四棱锥E-ABCD中,△ABD是正三角形,△BCD是等腰三角形,∠BCD=120°,EC⊥BD.
如图,在四棱锥E-ABCD中,△ABD是正三角形,△BCD是等腰三角形,∠BCD=120°,EC⊥BD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com