
分析 (1)由$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$=$\overrightarrow{0}$可得P为△ABC的重心,设A(x,y),则P($\frac{x}{3},\frac{y}{3}$),再由|$\overrightarrow{QA}$|=|$\overrightarrow{QB}$|=|$\overrightarrow{QC}$|,知Q是△ABC的外心,Q在x轴上,再由$\overrightarrow{PQ}$∥$\overrightarrow{BC}$,可得Q($\frac{x}{3},0$),结合|$\overrightarrow{QA}$|=|$\overrightarrow{QC}$|求得顶点A的轨迹E的方程;
(2)F($\sqrt{2}$,0)恰为$\frac{{x}^{2}}{3}+{y}^{2}=1$的右焦点.当直线l1,l2的斜率存在且不为0时,设直线l1 的方程为my=x-$\sqrt{2}$.联立直线方程与椭圆方程,化为关于y的一元二次方程,利用根与系数的关系求得A、B的纵坐标得到和与积.
(ⅰ)根据焦半径公式得|A1B1|、|A2B2|,代入四边形面积公式再由基本不等式求得四边形A1A2B1B2的面积S的最小值;
(ⅱ)根据中点坐标公式得M、N的坐标,得到直线MN的方程,化简整理令y=0解得x值,可得直线MN恒过定点;当直线l1,l2有一条直线的斜率不存在时,另一条直线的斜率为0,直线MN即为x轴,过点($\frac{3\sqrt{2}}{4},0$).
解答 解:(1)由$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$=$\overrightarrow{0}$,得$\overrightarrow{PC}=-2\overrightarrow{PO}$,∴P为△ABC的重心,
设A(x,y),则P($\frac{x}{3},\frac{y}{3}$),由|$\overrightarrow{QA}$|=|$\overrightarrow{QB}$|=|$\overrightarrow{QC}$|,知Q是△ABC的外心,∴Q在x轴上,
由$\overrightarrow{PQ}$∥$\overrightarrow{BC}$,可得Q($\frac{x}{3},0$),由|$\overrightarrow{QA}$|=|$\overrightarrow{QC}$|,得$\sqrt{(\frac{x}{3})^{2}+1}=\sqrt{(x-\frac{x}{3})^{2}+{y}^{2}}$.
化简整理得:$\frac{{x}^{2}}{3}+{y}^{2}=1$(x≠0);
(2)F($\sqrt{2}$,0)恰为$\frac{{x}^{2}}{3}+{y}^{2}=1$的右焦点.
①当直线l1,l2的斜率存在且不为0时,设直线l1 的方程为my=x-$\sqrt{2}$.
联立$\left\{\begin{array}{l}{my=x-\sqrt{2}}\\{{x}^{2}+3{y}^{2}-3=0}\end{array}\right.$,得$({m}^{2}+3){y}^{2}+2\sqrt{2}my-1=0$.
设A(x1,y1),B(x2,y2),则${y}_{1}+{y}_{2}=\frac{-2\sqrt{2}m}{{m}^{2}+3},{y}_{1}{y}_{2}=\frac{-1}{{m}^{2}+3}$.
(ⅰ)根据焦半径公式得:$|{A}_{1}{B}_{1}|=2\sqrt{3}-\frac{\sqrt{2}}{\sqrt{3}}({x}_{1}+{x}_{2})$,
又${x}_{1}+{x}_{2}=m{y}_{1}+\sqrt{2}+m{y}_{2}+\sqrt{2}=m({y}_{1}+{y}_{2})$$+2\sqrt{2}$=$\frac{-2\sqrt{2}{m}^{2}}{{m}^{2}+3}+2\sqrt{2}=\frac{6\sqrt{2}}{{m}^{2}+3}$.
∴$|{A}_{1}{B}_{1}|=2\sqrt{3}-\frac{4\sqrt{3}}{{m}^{2}+3}$=$\frac{2\sqrt{3}({m}^{2}+1)}{{m}^{2}+3}$,同理|A2B2|=$\frac{2\sqrt{3}(\frac{1}{{m}^{2}}+1)}{\frac{1}{{m}^{2}}+3}$=$\frac{2\sqrt{3}({m}^{2}+1)}{3{m}^{2}+1}$.
则$S=6\frac{({m}^{2}+1)^{2}}{({m}^{2}+3)(3{m}^{2}+1)}$≥6$\frac{(m+1)^{2}}{(\frac{4({m}^{2}+1)}{2})^{2}}=\frac{3}{2}$.
当m2+3=3m2+1,即m=±1时取等号.
(ⅱ)根据中点坐标公式得:M($\frac{3\sqrt{2}}{{m}^{2}+3},\frac{-\sqrt{2}m}{{m}^{2}+3}$),同理可得N($\frac{3\sqrt{2}{m}^{2}}{3{m}^{2}+1},\frac{\sqrt{2}m}{3{m}^{2}+1}$).
则直线MN的斜率为kMN=$\frac{\frac{\sqrt{2}m}{3{m}^{2}+3}-\frac{-\sqrt{2}m}{{m}^{2}+3}}{\frac{3\sqrt{2}{m}^{2}}{3{m}^{2}+1}-\frac{3\sqrt{2}}{{m}^{2}+3}}$=$\frac{4m}{3({m}^{2}-1)}$.
∴直线MN的方程为$y-\frac{-\sqrt{2}m}{{m}^{2}+3}=\frac{4m}{3({m}^{2}-1)}(x-\frac{3\sqrt{2}}{{m}^{2}+3})$,
化简整理得:$3y{m}^{4}+(3\sqrt{2}-4x){m}^{3}+6y{m}^{2}+3(3\sqrt{2}-4x)m-9y=0$.
令y=0,解得x=$\frac{3\sqrt{2}}{4}$,∴直线MN恒过定点($\frac{3\sqrt{2}}{4},0$).
②当直线l1,l2有一条直线的斜率不存在时,另一条直线的斜率为0,
直线MN即为x轴,过点($\frac{3\sqrt{2}}{4},0$).
综上,S的最小值为$\frac{3}{2}$,直线MN过定点($\frac{3\sqrt{2}}{4},0$).
点评 本题考查轨迹方程的求法,考查椭圆的简单性质,训练了直线与椭圆位置关系的应用,考查计算能力,是压轴题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
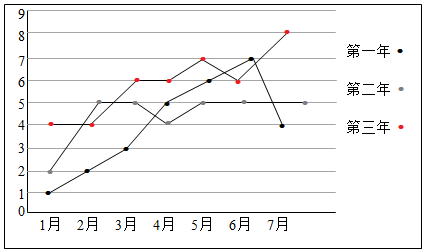
| 月份x | 1 | 2 | 3 | 4 |
| 利润y(单位:百万元) | 4 | 4 | 6 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | N⊆M | B. | M⊆∁RN | C. | M∩N=∅ | D. | M∪N=R |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com