
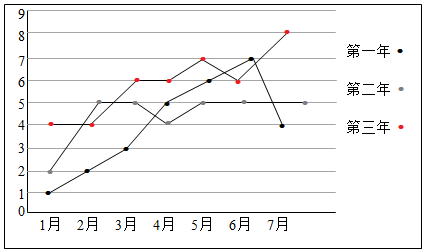
| 月份x | 1 | 2 | 3 | 4 |
| 利润y(单位:百万元) | 4 | 4 | 6 | 6 |
分析 (1)结合图象读出结论即可;(2)根据图象累加判断结论即可;(3)分别求出对应的系数$\widehat{a}$,$\widehat{b}$的值,代入回归方程即可.
解答 解:(1)由折线图可知5月和6月的平均利润最高.…(2分)
(2)第1年前7个月的总利润为1+2+3+5+6+7+4=28(百万元),…(3分)
第2年前7个月的总利润为2+5+5+4+5+5+5=31(百万元),…(4分)
第3年前7个月的总利润为4+4+6+6+7+6+8=41百万元),…(5分)
所以这3年的前7个月的总利润呈上升趋势.…(7分)
(3)∵$\overline x=2.5$,$\overline y=5,{1^2}+{2^2}+{3^2}+{4^2}=30$,1×4+2×4+3×6+4×6=54,
∴$\widehatb=\frac{54-4×2.5×5}{{30-4×{{2.5}^2}}}=0.8$,…(9分)
∴$\widehata=5-2.5×8=3$,…(10分)
∴$\widehaty=0.8x+3$,…(11分)
当x=8时,$\widehaty=0.8×8+3=9.4$(百万元),
∴估计8月份的利润为940万元.…(12分)
点评 本题考查了回归方程问题,考查折线图以及计算能力,是一道中档题.


科目:高中数学 来源: 题型:解答题
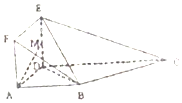 如图,在多面体ABCDEF中,平面ADEF与平面ABCD垂直,ADEF是正方形,在直角梯形ABCD中,AB∥CD,AB⊥AD,且AB=AD=$\frac{1}{2}$CD=1,M为线段ED的中点.
如图,在多面体ABCDEF中,平面ADEF与平面ABCD垂直,ADEF是正方形,在直角梯形ABCD中,AB∥CD,AB⊥AD,且AB=AD=$\frac{1}{2}$CD=1,M为线段ED的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)=\frac{{{x^2}-2x}}{x-2}$ | B. | f(x)=x-$\frac{1}{x}$ | C. | f(x)=2x-2-x | D. | f(x)=x|sinx| |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
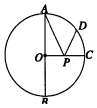 如图所示,AB为⊙O的直径,AB=2,OC是⊙O的半径,OC⊥AB,点D在$\widehat{AC}$上,$\widehat{AD}$=2$\widehat{CD}$,点P是OC上一动点,则PA+PD的最小值为$\sqrt{3}$.
如图所示,AB为⊙O的直径,AB=2,OC是⊙O的半径,OC⊥AB,点D在$\widehat{AC}$上,$\widehat{AD}$=2$\widehat{CD}$,点P是OC上一动点,则PA+PD的最小值为$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com