
分析 (1)利用曲线y=f(x)在x=1处的切线与直线x-2y-7=0垂直,求出a的值,利用导数的正负求f(x)的单调区间;
(2)分充分性、必要性证明,即可证明f(x)≥1恒成立的充要条件是a=1.
解答 (1)解:因为$f'(x)=1-\frac{a}{x}$,所以f'(1)=1-a,
所以$\frac{1}{2}(1-a)=-1$,解得a=3.
令$f'(x)=1-\frac{3}{x}>0$,得x>3,所以f(x)得单调递增区间为(3,+∞),
令$f'(x)=1-\frac{3}{x}<0$,得0<x<3,所以f(x)的单调递减区间为(0,3).
(2)证明:①充分性.
当a=1时,f(x)=x-lnx,$f'(x)=1-\frac{1}{x}=\frac{x-1}{x}$,
所以当x>1时,f'(x)>0,所以函数f(x)在(1,+∞)上是增函数;
当0<x<1时,f'(x)<0,所以函数f(x)在(0,1)上是减函数.
所以f(x)≥f(1)=1.
②必要性.$f'(x)=1-\frac{a}{x}=\frac{x-a}{x}$,其中x>0.
(i)当a≤0时,f'(x)>0恒成立,所以函数f(x)在(0,+∞)上是增函数.
而f(1)=1,所以当x∈(0,1)时,f(x)<1,与f(x)≥1恒成立矛盾,
所以a≤0不满足题意.
(ii)当a>0时,
因为当x>a时,f'(x)>0,所以函数f(x)在(a,+∞)上是增函数;
当0<x<a时,f'(x)<0,所以函数f(x)在(0,a)上是减函数.
所以f(x)≥f(a)=a-alna,
因为f(1)=1,所以当a≠1时,f(a)<f(1)=1,此时与f(x)≥1恒成立矛盾,
所以a=1.
综上所述,f(x)≥1恒成立的充要条件是a=1.
点评 本题考查导数知识的综合运用,考查函数的单调性,考查充要性的证明,属于中档题.


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {3} | B. | {7,8} | C. | {7,8,9} | D. | {1,2,3,4,5,6} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,\frac{1}{2}]$ | B. | $[{0,\frac{1}{2}}]$ | C. | $[\frac{1}{2},+∞)$ | D. | $[{\frac{1}{2},1}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | arccos(sinx) | B. | π+arccos(sinx) | C. | -arccos(sinx) | D. | -π-arccos(sinx) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{17}{3}$ | B. | $\frac{22}{3}$ | C. | $\frac{32}{3}$ | D. | $\frac{35}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
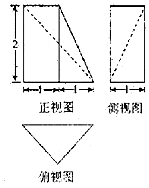
| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | 2 | D. | $\frac{8}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com