
分析 (1)设椭圆方程为:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,求出左焦点F1(-c,0),右焦点F2(c,0),B(0,b),A(a,0),推出$D({\frac{a}{2},\frac{b}{2}})$,利用${k_{OD}}•{k_{AB}}=\frac{b}{a}•({-\frac{b}{a}})=-\frac{1}{2}$知,a2=2b2,结合三角形的面积,求出a,b即可得到椭圆方程.
(2)由上知F1(-2,0),设过F1的直线l的方程为:x+2=my,联立直线与椭圆方程,消去x,设M(x1,y1),N(x2,y2),利用韦达定理弦长公式,表示三角形的面积,然后求解即可.
解答 解:(1)设椭圆方程为:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,
左焦点F1(-c,0),右焦点F2(c,0),B(0,b),A(a,0),
则$D({\frac{a}{2},\frac{b}{2}})$,由已知${k_{OD}}•{k_{AB}}=\frac{b}{a}•({-\frac{b}{a}})=-\frac{1}{2}$知,a2=2b2,
又${S_{△AOB}}=\frac{1}{2}ab=2\sqrt{2}⇒ab=4\sqrt{2}$,解得a2=8,b2=4,
所以椭圆方程为:$\frac{x^2}{8}+\frac{y^2}{4}=1$.
(2)由上知F1(-2,0),设过F1的直线l的方程为:x+2=my,
由$\left\{\begin{array}{l}x=my-2\\{x^2}+2{y^2}=8\end{array}\right.⇒({{m^2}+2}){y^2}-4my-4=0$,
设M(x1,y1),N(x2,y2),则$\left\{\begin{array}{l}{y_1}+{y_2}=\frac{4m}{{{m^2}+2}}\\{y_1}{y_2}=-\frac{4}{{{m^2}+2}}\end{array}\right.$,又因为${S_{△M{F_2}N}}=\frac{1}{2}•2c•|{{y_1}-{y_2}}|=2\sqrt{{{({\frac{4m}{{{m^2}+2}}})}^2}-4•({-\frac{4}{{{m^2}+2}}})}=\frac{16}{3}$;
化简得2m4-m2-1=0⇒m2=1或${m^2}=-\frac{1}{2}$(舍去),
故m=±1,此时直线l的方程为:x-y+2=0或x+y+2=0,
易知F2(2,0)到直线l的距离为圆的半径,即$r=2\sqrt{2}$,
所以所求圆的方程为:(x-2)2+y2=8.
点评 本题考查椭圆方程的求法,直线与椭圆的位置关系的综合应用,考查转化思想以及计算能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
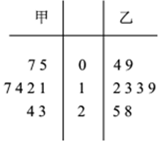 如图是甲、乙两个商场统计同一时间段各自每天的销售额(单位:万元)的茎叶图,假设销售额的中位数为m,平均值为$\overline{x}$,则下列正确的是( )
如图是甲、乙两个商场统计同一时间段各自每天的销售额(单位:万元)的茎叶图,假设销售额的中位数为m,平均值为$\overline{x}$,则下列正确的是( )| A. | m甲=m乙,$\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$ | B. | m甲=m乙,$\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$ | ||
| C. | m甲>m乙,$\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$ | D. | m甲<m乙,$\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
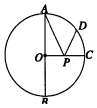 如图所示,AB为⊙O的直径,AB=2,OC是⊙O的半径,OC⊥AB,点D在$\widehat{AC}$上,$\widehat{AD}$=2$\widehat{CD}$,点P是OC上一动点,则PA+PD的最小值为$\sqrt{3}$.
如图所示,AB为⊙O的直径,AB=2,OC是⊙O的半径,OC⊥AB,点D在$\widehat{AC}$上,$\widehat{AD}$=2$\widehat{CD}$,点P是OC上一动点,则PA+PD的最小值为$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 22 | B. | 20 | C. | 17 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
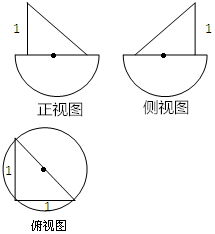 已知某几何体的三视图如图所示,其中正视图、侧视图均由直角三角形中与半圆构成,俯视图由圆和内接三角形构成,根据图中的数据可得几何体的表面积为( )
已知某几何体的三视图如图所示,其中正视图、侧视图均由直角三角形中与半圆构成,俯视图由圆和内接三角形构成,根据图中的数据可得几何体的表面积为( )| A. | 1+$\frac{\sqrt{3}+3π}{2}$ | B. | $\frac{1+\sqrt{3}+π}{2}$ | C. | $\frac{1+\sqrt{3}+3π}{2}$ | D. | $\frac{3+\sqrt{3}+3π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,\frac{1}{2}]$ | B. | $[{0,\frac{1}{2}}]$ | C. | $[\frac{1}{2},+∞)$ | D. | $[{\frac{1}{2},1}]$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com