Question

18．形如y=$\frac{b}{|x|-c}$（c＞0，b＞0）的函数因其图象类似于汉字中的“囧”字，故我们把其生动地称为“囧函数”．若函数f（x）=log_a（x²+x+1）（a＞0，a≠1）有最小值，则当c，b的值分别为方程x²+y²-2x-2y+2=0中的x，y时的“囧函数”与函数y=log_a|x|的图象交点个数为（　　）

• A． 1
• B． 2
• C． 4
• D． 6

Answer 1

分析 由题意可得a＞1，c=b=1，这时“囧函数”为$y=\frac{1}{|x|-1}$，它与函数y=log_a|x|在同一坐标系内的图象如图所示，数形结合求得它们的图象交点个数．

解答 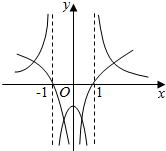解：令u=x²+x+1，则$f（x）={log_a}（{{x^2}+x+1}）$是y=log_au与u=x²+x+1复合函数，
∵$u={（x+\frac{1}{2}）^2}+\frac{3}{4}≥\frac{3}{4}$，当y=log_au是增函数，$u∈[\frac{3}{4}，+∞）$时有最小值，
所以，a＞1；x²+y²-2x-2y+2=0，
即（x-1）²+（y-1）²=0，可得x=y=1，
所以，c=b=1，这时“囧函数”为$y=\frac{1}{|x|-1}$，
它与函数y=log_a|x|在同一坐标系内的图象如图所示，
数形结合可得它们的图象交点个数为4，
故选：C．

点评 本题主要考查函数的图象特征，两个函数的图象交点个数，体现了转化、数形结合的数学思想，属于中档题．