
已知椭圆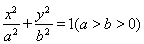 的一个焦点
的一个焦点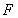 与抛物线
与抛物线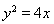 的焦点重合,且截抛物线的准线所得弦长为
的焦点重合,且截抛物线的准线所得弦长为 ,倾斜角为
,倾斜角为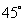 的直线
的直线 过点
过点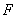 .
.
(1)求该椭圆的方程;
(2)设椭圆的另一个焦点为 ,问抛物线
,问抛物线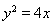 上是否存在一点
上是否存在一点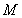 ,使得
,使得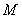 与
与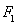 关于直线
关于直线 对称,若存在,求出点
对称,若存在,求出点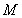 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
(1)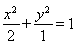 ;(2)抛物线
;(2)抛物线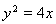 上存在一点
上存在一点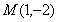 ,使得
,使得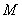 与
与 关于直线
关于直线 对称.
对称.
【解析】
试题分析:(1)求椭圆的方程,可利用待定系数法求出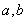 的值即可,首先确定抛物线
的值即可,首先确定抛物线 的焦点
的焦点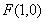 与准线方程为
与准线方程为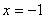 ,利用椭圆焦点
,利用椭圆焦点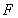 与抛物线
与抛物线 的焦点重合,得
的焦点重合,得 ,且截抛物线的准线所得弦长为
,且截抛物线的准线所得弦长为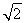 ,得交点为
,得交点为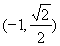 ,建立方程,求出
,建立方程,求出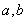 的值,即可求得椭圆的方程;(2)根据倾斜角为
的值,即可求得椭圆的方程;(2)根据倾斜角为 的直线
的直线 过点
过点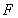 ,可得直线
,可得直线 的方程
的方程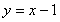 ,由(1)知椭圆的另一个焦点为
,由(1)知椭圆的另一个焦点为 ,利用
,利用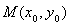 与
与 关于直线
关于直线 对称,利用对称,可求得
对称,利用对称,可求得 的坐标,由此可得结论.
的坐标,由此可得结论.
试题解析:(1)抛物线 的焦点为
的焦点为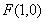 ,准线方程为
,准线方程为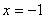 ,
,
∴ 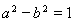 ① 2分
① 2分
又椭圆截抛物线的准线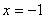 所得弦长为
所得弦长为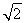 ,
,
∴ 得上交点为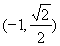 ,∴
,∴  ② 4分
② 4分
由①代入②得 ,解得
,解得 或
或 (舍去),
(舍去),
从而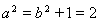
∴该椭圆的方程为该椭圆的方程为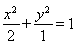 6分
6分
(2)∵ 倾斜角为 的直线
的直线 过点
过点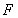 ,
,
∴ 直线 的方程为
的方程为 ,即
,即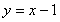 , 7分
, 7分
由(1)知椭圆的另一个焦点为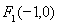 ,设
,设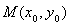 与
与 关于直线
关于直线 对称,则得
对称,则得 , 9分
, 9分
解得 ,即
,即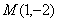 , 2分
, 2分
又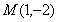 满足
满足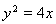 ,故点
,故点 在抛物线上。所以抛物线
在抛物线上。所以抛物线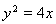 上存在一点
上存在一点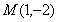 ,使得
,使得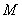 与
与 关于直线
关于直线 对称。 13分
对称。 13分
考点:直线与圆锥曲线的综合问题;椭圆的标准方程;抛物线的简单性质.


科目:高中数学 来源:2013-2014学年高中数学人教A版选修4-1知能达标2-4练习卷(解析版) 题型:选择题
如图所示,AB是⊙O的直径,EF切⊙O于C,AD⊥EF于D,AD=2,AB=6,则AC的长为
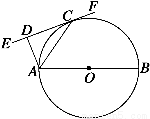
A.2 B.3
C.2 D.4
D.4
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高中数学人教A版选修4-1知能达标1-3练习卷(解析版) 题型:解答题
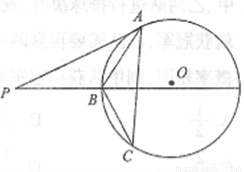
(拓展深化)如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=α.且DM交AC于F,ME交BC于G,
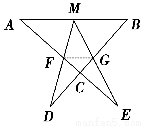
(1)写出图中三对相似三角形,并证明其中的一对;
(2)连接FG,如果α=45°,AB=4 ,AF=3,求FG的长.
,AF=3,求FG的长.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高中数学人教A版选修4-1知能达标1-2练习卷(解析版) 题型:选择题
如图所示,AD是△ABC的中线,E是CA边的三等分点,BE交AD于点F,则AF∶FD为
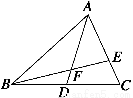
A.2∶1 B.3∶1
C.4∶1 D.5∶1
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高中数学人教A版选修4-1知能达标1-1练习卷(解析版) 题型:填空题
在梯形ABCD中,M、N分别是腰AB和腰CD的中点,且AD=2,BC=4,则MN=________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西西安第一中学高三第二学期第二次模拟考试理科数学试卷(解析版) 题型:填空题
如图所示,过圆O外一点P分别作圆的切线和割线交圆于A,B,且PB = 7, C是圆上一点使得BC = 5,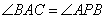 ,则AB =____________
,则AB =____________
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西西安第一中学高三第二学期第二次模拟考试理科数学试卷(解析版) 题型:选择题
规定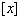 表示不超过
表示不超过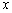 的最大整数,例如:[3.1]=3,[
的最大整数,例如:[3.1]=3,[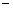 2.6]=
2.6]=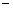 3,[
3,[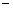 2]=
2]=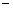 2;若
2;若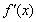 是函数
是函数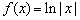 导函数,设
导函数,设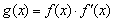 ,则函数
,则函数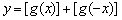 的值域是( )
的值域是( )
A.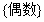 B.
B.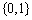 C.
C.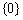 D.
D.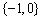
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西西安第一中学高三第二学期第二次模拟考试文科数学试卷(解析版) 题型:填空题
如图,在圆O中,直径AB与弦CD垂直,垂足为E,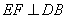 ,垂足为F,若
,垂足为F,若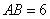 ,
,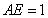 ,则
,则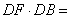
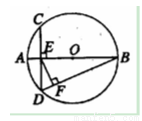
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com