
【题目】函数f(x)=cos( ![]() x+
x+ ![]() )的图象向右平移φ(φ>0)个单位,所得函数图象关于y轴对称,则φ的最小值为 .
)的图象向右平移φ(φ>0)个单位,所得函数图象关于y轴对称,则φ的最小值为 .
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(a﹣ ![]() )(a∈R).若关于x的方程ln[(4﹣a)x+2a﹣5]﹣f(x)=0的解集中恰好有一个元素,则实数a的取值范围为 .
)(a∈R).若关于x的方程ln[(4﹣a)x+2a﹣5]﹣f(x)=0的解集中恰好有一个元素,则实数a的取值范围为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥S﹣ABC中,E为棱SC的中点,若AC=2 ![]() ,SA=SB=AB=BC=SC=2,则异面直线AC与BE所成的角为( )
,SA=SB=AB=BC=SC=2,则异面直线AC与BE所成的角为( ) 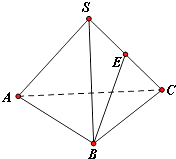
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆 ![]() 的离心率
的离心率 ![]() ,椭圆上一点A到椭圆C两焦点的距离之和为4.
,椭圆上一点A到椭圆C两焦点的距离之和为4.
(1)求椭圆C的方程;
(2)直线l与椭圆交于A,B两点,且AB中点为 ![]() ,求直线l方程.
,求直线l方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:
(1)利用计算机产生0~1之间的均匀随机数a,则事件“3a﹣1>0”发生的概率为 ![]() ;
;
(2)“x+y≠0”是“x≠1或y≠﹣1”的充分不必要条件;
(3)如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β;
(4)设 ![]() 是非零向量,已知命题p:若
是非零向量,已知命题p:若 ![]() ,
, ![]() ,则
,则 ![]() ;命题q:若
;命题q:若 ![]() ,则
,则 ![]() ,则“p∨q”是真命题.
,则“p∨q”是真命题.
其中说法正确的个数是( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)对任意的x都有f(x+2)﹣f(x)=﹣4x+4,且f(0)=0.
(1)求函数f(x)的解析式;
(2)设函数g(x)=f(x)+m,(m∈R). ①若存在实数a,b(a<b),使得g(x)在区间[a,b]上为单调函数,且g(x)取值范围也为[a,b],求m的取值范围;
②若函数g(x)的零点都是函数h(x)=f(f(x))+m的零点,求h(x)的所有零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机械厂今年进行了五次技能考核,其中甲、乙两名技术骨干得分的平均分相等,成绩统计情况如茎叶图所示(其中a是0﹣9的某个整数 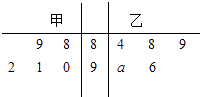
(1)若该厂决定从甲乙两人中选派一人去参加技能培训,从成绩稳定性角度考虑,你认为谁去比较合适?
(2)若从甲的成绩中任取两次成绩作进一步分析,在抽取的两次成绩中,求至少有一次成绩在(90,100]之间的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com