
分析 利用余弦定理,结合AC=$\sqrt{2}$AB,即可求出BD.
解答  解:设BD=x,则DC=2x,
解:设BD=x,则DC=2x,
由余弦定理可得AB=$\sqrt{{x}^{2}+2-2\sqrt{2}xcos135°}$=$\sqrt{{x}^{2}+2x+2}$,
AC=$\sqrt{4{x}^{2}+2-4\sqrt{2}xcos45°}$=$\sqrt{4{x}^{2}-4x+2}$,
∵AC=$\sqrt{2}$AB,
∴$\sqrt{4{x}^{2}-4x+2}$=$\sqrt{2}×$$\sqrt{{x}^{2}+2x+2}$,整理可得:x2-4x-1=0,
解得:x=2+$\sqrt{5}$,或2-$\sqrt{5}$(舍去).
故答案为:2+$\sqrt{5}$.
点评 本题考查解三角形的实际应用,考查余弦定理,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
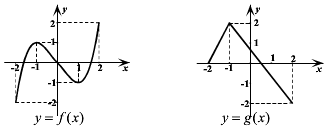
| A. | ②③④ | B. | ①④ | C. | ②③ | D. | ①②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,+∞) | B. | [2,+∞) | C. | [2,4] | D. | [2,4) |
查看答案和解析>>
科目:高中数学 来源:2017届山东临沭一中高三上学期10月月考数学(文)试卷(解析版) 题型:选择题
已知变量 、
、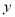 满足约束条件
满足约束条件 若目标函数
若目标函数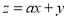 仅在点
仅在点 取到最大值,则实数
取到最大值,则实数 的取值范围是( )
的取值范围是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com