
【题目】已知函数![]() .
.
(1)讨论![]() 在
在![]() 极值点个数;
极值点个数;
(2)证明:不等式![]() 在
在![]() 恒成立.
恒成立.
附:![]() .
.
【答案】(1)有两个极值点(2)证明见解析;
【解析】
(1)求出函数的导函数,分![]() ,
,![]() 以及
以及![]() ,判断函数的单调性,进而得出极值点情况;
,判断函数的单调性,进而得出极值点情况;
(2)分![]() ,
,![]() ,结合零点存在性定理以及放缩思想得证.
,结合零点存在性定理以及放缩思想得证.
解:(1)由![]() ,求导数
,求导数![]() ,设
,设![]()
①在![]() 时,则
时,则![]()
![]() ,知
,知![]() 在
在![]() 递减,
递减,
![]() 存在
存在![]() 使得
使得![]()
在![]() 时,
时,![]() ,在
,在![]() 时,
时,![]()
![]() 为
为![]() 的极大值点.
的极大值点.
②在![]() 时,
时,![]() 有
有![]()
![]() 在
在![]() 上恒成立,
上恒成立,![]() 在
在![]() 上递减
上递减
![]() 此时无极值.
此时无极值.
③在![]() 时,
时,![]()
![]() ,在
,在![]() 上恒成立.
上恒成立.
![]() 在
在![]() 上递增,
上递增,
因此存在唯一![]() ,使得
,使得![]()
在![]() 时,
时,![]() ,在
,在![]() 时,
时,![]()
![]() 为
为![]() 极小值点.
极小值点.
综合讨论![]() 在
在![]() 有两个极值点.
有两个极值点.
(2)令![]() ,则
,则![]()
①若![]() 时,
时,![]() ,而
,而![]()
所以![]() ,
,![]() 在
在![]() 递减,
递减,
所以![]()
②若![]() ,
,![]() ,
, ,
,![]()
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 递增,
递增,
所以存在唯一![]() 使得
使得![]() ,
,
当![]() 时,
时,![]() 递减;当
递减;当![]() 时,
时,![]() 递增,
递增,
故
下面证明:![]() 在
在![]() 上恒成立
上恒成立
记![]() ,
,![]()
则![]() ,所以
,所以![]() 在
在![]() 递增,
递增,
于是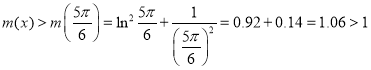 ,
,
从而可知 ,
,
综合①②可知![]() 在
在![]() 上恒成立.
上恒成立.


科目:高中数学 来源: 题型:
【题目】某“芝麻开门”娱乐活动中,共有![]() 扇门,游戏者根据规则开门,并根据打开门的数量获取相应奖励.已知开每扇门相互独立,且规则相同,开每扇门的规则是:从给定的
扇门,游戏者根据规则开门,并根据打开门的数量获取相应奖励.已知开每扇门相互独立,且规则相同,开每扇门的规则是:从给定的![]() 把钥匙(其中有且只有
把钥匙(其中有且只有![]() 把钥匙能打开门)中,随机地逐把抽取钥匙进行试开,钥匙使用后不放回.若门被打开,则转为开下一扇门;若连续
把钥匙能打开门)中,随机地逐把抽取钥匙进行试开,钥匙使用后不放回.若门被打开,则转为开下一扇门;若连续![]() 次未能打开,则放弃这扇门,转为开下一扇门;直至
次未能打开,则放弃这扇门,转为开下一扇门;直至![]() 扇门都进行了试开,活动结束.
扇门都进行了试开,活动结束.
(1)设随机变量![]() 为试开第一扇门所用的钥匙数,求
为试开第一扇门所用的钥匙数,求![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
(2)求恰好成功打开![]() 扇门的概率.
扇门的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以平面直角坐标系![]() 的原点为极点,
的原点为极点,![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,已知过点
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,已知过点![]() 且斜率为1的直线
且斜率为1的直线![]() 与曲线
与曲线![]() :
:![]() (
(![]() 是参数)交于
是参数)交于![]() 两点,与直线
两点,与直线![]() :
:![]() 交于点
交于点![]() .
.
(1)求曲线![]() 的普通方程与直线
的普通方程与直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 的中点为
的中点为![]() ,比较
,比较![]() 与
与![]() 的大小关系,并说明理由.
的大小关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴是短轴的两倍,以短轴一个顶点和长轴一个顶点为端点的线段作直径的圆的周长等于
的长轴是短轴的两倍,以短轴一个顶点和长轴一个顶点为端点的线段作直径的圆的周长等于![]() ,直线l与椭圆C交于
,直线l与椭圆C交于![]() 两点,其中直线l不过原点.
两点,其中直线l不过原点.
(1)求椭圆C的方程;
(2)设直线![]() 的斜率分别为
的斜率分别为![]() ,其中
,其中![]() 且
且![]() .记
.记![]() 的面积为S.分别以
的面积为S.分别以![]() 为直径的圆的面积依次为
为直径的圆的面积依次为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高三数学考试中,一般有一道选做题,学生可以从选修4-4和选修4-5中任选一题作答,满分10分.某高三年级共有1000名学生参加了某次数学考试,为了了解学生的作答情况,计划从该年级1000名考生成绩中随机抽取一个容量为10的样本,为此将1000名考生的成绩按照随机顺序依次编号为000~999.
(1)若采用系统抽样法抽样,从编号为000~999的成绩中随机确定的编号为026,求样本中的最大编号.
(2)若采用分层抽样法,按照学生选择选修4-4或选修4-5的情况将成绩分为两层,已知该校共有600名考生选择了选修4-4,400名考生选择了选修4-5,在选取的样本中,选择选修4-4的平均得分为6分,方差为2,选择选修4-5的平均得分为5分,方差为0.75.用样本估计该校1000名考生选做题的平均得分和得分的方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC﹣A1B1C1中,∠ACB=90°,∠ABC=45°,AB=AA1=2,P为CC1的中点.
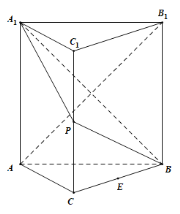
(1)证明:AB1⊥平面PA1B;
(2)设E为BC的中点,线段AB1上是否存在一点Q,使得QE∥平面A1ACC1?若存在,求四棱锥Q﹣AA1C1C的体积;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,过
,过![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 的周长为8.
的周长为8.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)问:![]() 的内切圆面积是否有最大值?若有,试求出最大值;若没有,说明理由.
的内切圆面积是否有最大值?若有,试求出最大值;若没有,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com