Question

17．设点P是圆x²+y²=4上的任一点，定点D的坐标为（8，0），若点M满足$\overrightarrow{PM}$=2$\overrightarrow{MD}$，当点P在圆上运动时，求点M的轨迹方程．

Answer 1

分析 设出M、P的坐标，利用$\overrightarrow{PM}$=2$\overrightarrow{MD}$，把P的坐标用M的坐标表示，然后代入已知圆的方程求得点M的轨迹方程．

解答 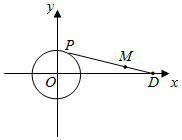解：如图，设M（x，y），P（x₀，y₀），又D（8，0），
由$\overrightarrow{PM}$=2$\overrightarrow{MD}$，得（x-x₀，y-y₀）=（16-2x，-2y），
∴$\left\{\begin{array}{l}{x-{x}_{0}=16-2x}\\{y-{y}_{0}=-2y}\end{array}\right.$，即$\left\{\begin{array}{l}{{x}_{0}=3x-16}\\{{y}_{0}=3y}\end{array}\right.$，
∵点P（x₀，y₀）在圆x²+y²=4上，
∴${{x}_{0}}^{2}+{{y}_{0}}^{2}=4$，即（3x-16）²+（3y）²=4，
∴$（x-\frac{16}{3}）^{2}+{y}^{2}=\frac{4}{9}$．
故点M的轨迹方程为$（x-\frac{16}{3}）^{2}+{y}^{2}=\frac{4}{9}$．

点评 本题考查轨迹方程，训练了利用代入法求曲线的方程，是中档题．