
分析 分别求出p,q为真时的a的范围,通过讨论p,q的真假,求出a的范围即可.
解答 解:由a>0,命题p:函数y=lg(ax2-x+$\frac{a}{16}$)的定义域为R,
可知,△=1-$\frac{{a}^{2}}{4}$<0,解得a>2.
因此,命题p为真时,a>2.
对于命题q:当x∈[$\frac{1}{2}$,2]时,函数y=x+$\frac{1}{x}$>$\frac{1}{a}$恒成立,
即函数y=x+$\frac{1}{x}$在x∈[$\frac{1}{2}$,2]时的最小值ymin>$\frac{1}{a}$,
∵ymin=2,∴$\frac{1}{a}$<2.又a>0,∴a>$\frac{1}{2}$.
因此,命题q为真时,a>$\frac{1}{2}$.
∵命题“p∨q”为真命题,命题“p∧q”为假命题,
∴命题p与q中一个是真命题,一个是假命题.
当p真q假时,可得a∈∅;
当p假q真时,可得$\frac{1}{2}$<a≤2.
综上所述,a的取值范围为($\frac{1}{2}$,2].
点评 本题考查了复合命题的判断,考查对数函数以及函数最值问题,是一道中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
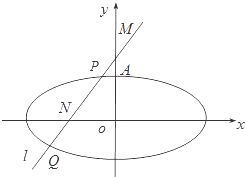 已知F1,F2,A分别为椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左右焦点及上顶点△AF1F2的面积为4$\sqrt{3}$且椭圆的离心率等于$\frac{{\sqrt{3}}}{2}$,过点M(0,4)的直线l与椭圆相交于不同的两点P、Q,点N在线段PQ上.
已知F1,F2,A分别为椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左右焦点及上顶点△AF1F2的面积为4$\sqrt{3}$且椭圆的离心率等于$\frac{{\sqrt{3}}}{2}$,过点M(0,4)的直线l与椭圆相交于不同的两点P、Q,点N在线段PQ上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,-2]∪[\frac{3}{2},+∞)$ | B. | $(-∞,-\frac{3}{2}]∪[2,+∞)$ | C. | $(-∞,-\frac{9}{2}]∪[6,+∞)$ | D. | $(-∞,-6]∪[\frac{9}{2},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com