
【题目】已知函数f(x)=5x+x-2,g(x)=log5x+x-2的零点分别为x1,x2,则x1+x2的值为________.
【答案】2
【解析】令f(x)=0,g(x)=0,得5x=-x+2,log5x=-x+2.作出函数y=5x,y=log5x,y=-x+2的图象,如图所示,因为函数f(x)=5x+x-2,g(x)=log5x+x-2的零点分别为x1,x2,所以x1是函数y=5x的图象与直线y=-x+2交点A的横坐标,x2是函数y=log5x的图象与直线y=-x+2交点B的横坐标.
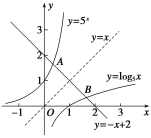
因为y=5x与y=log5x的图象关于y=x对称,直线y=-x+2也关于y=x对称,且直线y=-x+2与它们都只有一个交点,故这两个交点关于y=x对称.又线段AB的中点是y=x与y=-x+2的交点,即(1,1),所以x1+x2=2.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
极坐标系的极点为直角坐标系![]() 的原点,极轴为
的原点,极轴为![]() 轴的正半轴,两种坐标系中的长度单位相同,已知曲线
轴的正半轴,两种坐标系中的长度单位相同,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的直角坐标方程;
的直角坐标方程;
(2)直线 (
(![]() 为参数)与曲线
为参数)与曲线![]() 交于
交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高职院校进行自主招生文化素质考试,考试内容为语文、数学、英语三科,总分为200分.现从上线的考生中随机抽取20人,将其成绩用茎叶图记录如下:
男 | 女 | |||||||||||
15 | 6 | |||||||||||
5 | 4 | 16 | 3 | 5 | 8 | |||||||
8 | 2 | 17 | 2 | 3 | 6 | 8 | 8 | 8 | ||||
6 | 5 | 18 | 5 | 7 | ||||||||
19 | 2 | 3 | ||||||||||
(Ⅰ)计算上线考生中抽取的男生成绩的方差![]() ;(结果精确到小数点后一位)
;(结果精确到小数点后一位)
(Ⅱ)从上述茎叶图180分以上的考生中任选2人作为考生代表出席座谈会,求所选考生恰为一男一女的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)满足f(logax)=![]() ·(x-
·(x-![]() )(其中a>0且a≠1).
)(其中a>0且a≠1).
(1)求函数f(x)的解析式,并判断其奇偶性和单调性;
(2)当x∈(-∞,2)时,f(x)-4的值恒为负数,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为推动乒乓球运动的发展,某乒乓球比赛允许不同协会的运动员组队参加.现有来自甲协会的运动员![]() 名,其中种子选手
名,其中种子选手![]() 名;乙协会的运动员
名;乙协会的运动员![]() 名,其中种子选手
名,其中种子选手![]() 名.从这
名.从这![]() 名运动员中随机选择
名运动员中随机选择![]() 人参加比赛.
人参加比赛.
(1)设![]() 为事件“选出的
为事件“选出的![]() 人中恰有
人中恰有![]() 名种子选手,且这
名种子选手,且这![]() 名种子选手来自同一个协会”求事件
名种子选手来自同一个协会”求事件![]() 发生的概率;
发生的概率;
(2)设![]() 为选出的
为选出的![]() 人中种子选手的人数,求随机变量
人中种子选手的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在[-1,1]上的奇函数,当x∈[-1,0]时,函数的解析式为f(x)=![]() (a∈R).
(a∈R).
(1)试求a的值;
(2)写出f(x)在[0,1]上的解析式;
(3)求f(x)在[0,1]上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
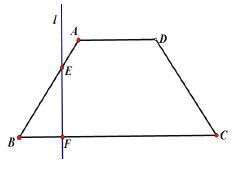
【题目】如图,已知底角为![]() 的等腰梯形
的等腰梯形![]() ,底边
,底边![]() 长为12,腰长为
长为12,腰长为![]() ,当一条垂直于底边
,当一条垂直于底边![]() (垂足为
(垂足为![]() )的直线
)的直线![]() 从左至右移动(与梯形
从左至右移动(与梯形![]() 有公共点)时,直线
有公共点)时,直线![]() 把梯形分成两部分.
把梯形分成两部分.
(1)令![]() ,试写出直线右边部分的面积
,试写出直线右边部分的面积![]() 与
与![]() 的函数解析式;
的函数解析式;
(2)在(1)的条件下,令![]() .构造函数
.构造函数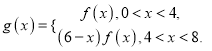
①判断函数![]() 在
在![]() 上的单调性;
上的单调性;
②判断函数![]() 在定义域内是否具有单调性,并说明理由.
在定义域内是否具有单调性,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车是城市慢行系统的一种模式创新,对于解决民众出行“最后一公里”的问题特别见效,由于停取方便、租用价格低廉,各色共享单车受到人们的热捧.某自行车厂为共享单车公司生产新样式的单车,已知生产新样式单车的固定成本为20000元,每生产一件新样式单车需要增加投入100元.根据初步测算,自行车厂的总收益(单位:元)满足分段函数![]() ,其中
,其中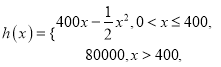
![]() 是新样式单车的月产量(单位:件),利润
是新样式单车的月产量(单位:件),利润![]() 总收益
总收益![]() 总成本.
总成本.
(1)试将自行车厂的利润![]() 元表示为月产量
元表示为月产量![]() 的函数;
的函数;
(2)当月产量为多少件时自行车厂的利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com