
| ʹ������ | 2 | 4 | 6 | 8 | 10 |
| �ۼ� | 16 | 13 | 9.5 | 7 | 4.5 |
���� �����ɱ������ݼ���$\overline{x}=\frac{1}{5}$����2+4+6+8+10��=6��$\overline{y}=\frac{1}{5}$����16+13+9.5+7+4.5��=10������ع�ϵ��������д���ع�ֱ�߷��̣�
����д��������z=y-w�����ö��κ�����ͼ�����������x=3ʱzȡ�����ֵ��
��� �⣺�����ɱ������ݵã�$\overline{x}=\frac{1}{5}$����2+4+6+8+10��=6��
$\overline{y}=\frac{1}{5}$����16+13+9.5+7+4.5��=10��
����С���˷����$\stackrel{��}{b}$=$\frac{2��16+4��13+6��9.5+8��7+10��4.5-5��6��10}{4+16+36+64+100-5��{6}^{2}}$=-1.45��
$\stackrel{��}{a}$=10-��-1.45����6=18.7��
����y����x�Ļع�ֱ�߷���Ϊ$\stackrel{��}{y}$=-1.45x+18.7��
����z=-1.45x+18.7-��0.05x2-1.75x+17.2��
=-0.05x2+0.3x+1.5
=-0.05��x-3��2+1.95��
����Ԥ�x=3ʱ����������zȡ�����ֵ��
���� ���⿼���˻ع�ֱ�߷��̵�����Ӧ�����⣬Ҳ�����˶��κ�����ͼ�������ʵ�Ӧ�����⣬�ǻ�����Ŀ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
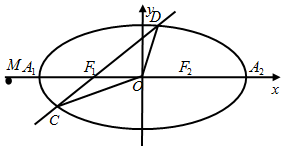 ���Ŀƣ���ͼ����֪��Բ������������ԭ�㣬����F1��F2����x���ϣ�����A1A2�ij�Ϊ4��x����һ��M��${-\frac{a^2}{c}��0}$����$|{\overrightarrow{M{A_1}}}|$=$2|{\overrightarrow{{A_1}{F_1}}}|$��
���Ŀƣ���ͼ����֪��Բ������������ԭ�㣬����F1��F2����x���ϣ�����A1A2�ij�Ϊ4��x����һ��M��${-\frac{a^2}{c}��0}$����$|{\overrightarrow{M{A_1}}}|$=$2|{\overrightarrow{{A_1}{F_1}}}|$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��x=0��x=1����x2-x��0 | B�� | ��x2-x=0����x=0��x=1 | ||
| C�� | ��x��0��x��1����x2-x��0 | D�� | ��x��0��x��1����x2-x��0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-8��-6] | B�� | ��-8��-6] | C�� | ��-�ޣ�-8���ȣ�-6��+�ޣ� | D�� | ��-�ޣ�-6] |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com