
记函数fn(x)=(1+x)n-1(n≥2,n∈N*)的导函数为f 'n(x),函数g(x)=fn(x)-nx.
(Ⅰ)讨论函数g(x)的单调区间和极值;
(Ⅱ)若实数x0和正数k满足: ,求证:0<x0<k.
,求证:0<x0<k.
(Ⅰ)由已知得,g(x)=fn(x)-nx=(1+x)n-1-nx,∴g'(x)=n[(1+x)n-1-1].
①当n≥2且n是偶数时,n-1是奇数,
由g'(x)>0,得x>0;由g'(x)<0,得x<0.
∴函数g(x)的递减区间是(-∞,0),递增区间是(0,+∞),
故函数g(x)的极小值为g(0)=0,没有极大值.
②当n≥2且n是奇数时,n-1是偶数,
由g'(x)>0,得x<-2或x>0;由g'(x)<0,得-2<x<0.
∴函数g(x)的递增区间是(-∞,-2),(0,+∞),递减区间是(-2,0),
故函数g(x)的极大值为g(-2)=2n-2,极小值为g(0)=0.
(Ⅱ)易知f 'n(x)=n(1+x)n-1,由 得:
得: ,
,
∴1+x0=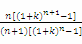 ,
,
x0=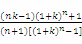 ,
,
显然(n+1)[(1+k)n-1]>0,
设h(k)=(nk-1)(1+k)n+1(k>0),
则h'(k)=n(1+k)n+n(1+k)n-1·(nk-1)=n(n+1)·k(1+k)n-1>0.
∴h(k)是(0,+∞)上的增函数,∴h(k)>h(0)=0.
故x0>0.
又x0-k=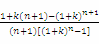 ,由(1)知,g(x)=(1+x)n-1-nx是(0,+∞)上的增函数,
,由(1)知,g(x)=(1+x)n-1-nx是(0,+∞)上的增函数,
故当x>0时,g(x)>g(0)=0,即(1+x)n>1+nx,
∴(1+k)n+1>1+(n+1)k,∴x0-k<0,x0<k.
综上所述,0<x0<k.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
设函数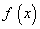 的定义域为D,如果
的定义域为D,如果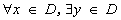 ,使得
,使得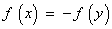 成立,则称函数
成立,则称函数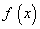 为“Ω函数” 给出下列四个函数:①
为“Ω函数” 给出下列四个函数:①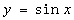 ;②
;② ;③
;③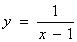 ;④
;④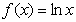 , 则其中“Ω函数”共有( )
, 则其中“Ω函数”共有( )
(A)1个 (B)2个 (C)3个 (D)4个
查看答案和解析>>
科目:高中数学 来源: 题型:
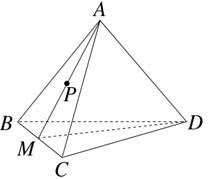
如图,在棱长为4的正四面体A-BCD中,M是BC的中点,点P在线段AM上运动(P不与A,M重合),过点P作直线l⊥平面ABC,l与平面BCD交于点Q,给出下列命题:①BC⊥平面AMD;②Q点一定在直线DM上;③VC-AMD=4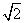 .其中正确命题的序号是( )
.其中正确命题的序号是( )
A.①② B.①③ C.②③ D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
已知f(x)=|x+1|+|x-2|,g(x)=|x+1|-|x-a|+a(a∈R).
(1)解不等式f(x)≤5;
(2)若不等式f(x)≥g(x)恒成立,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com