
已知函数 ,
,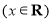 .
.
(1)证明:函数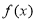 在区间
在区间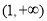 上为增函数,并指出函数
上为增函数,并指出函数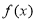 在区间
在区间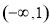 上的单调性.
上的单调性.
(2)若函数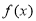 的图像与直线
的图像与直线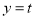 有两个不同的交点
有两个不同的交点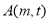 ,
, ,其中
,其中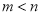 ,求
,求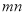 关于
关于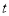 的函数关系式.
的函数关系式.
(3)求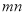 的取值范围.
的取值范围.
(1)见解析;(2)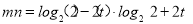 ;(3)
;(3)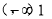 .
.
【解析】
试题分析:(1)用单调性的定义取值,做差,判断与零的关系,证明即可;(2)易知A(m,t),B(n,t)分别位于直线x=1的两侧,由m<n,得m<1<n,故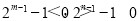 ,易得mn的表达式,解之即可;(3)分两种情况,当
,易得mn的表达式,解之即可;(3)分两种情况,当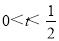 时,当
时,当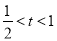 时,再由基本不等式可得.
时,再由基本不等式可得.
试题解析: (1)证明:任取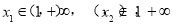 且
且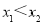
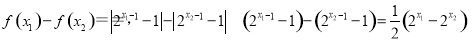
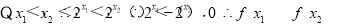
 所以f(x)在区间
所以f(x)在区间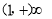 上为增函数.函数f(x)在区间
上为增函数.函数f(x)在区间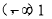 上为减函数.
上为减函数.
(2)因为函数f(x)在区间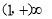 上为增函数,相应的函数值为
上为增函数,相应的函数值为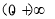 ,在区间
,在区间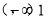 上为减函数,相应的函数值为(0,1),由题意函数f(x)的图象与直线y=t有两个不同的交点,故有t∈(0,1),易知A(m,t),B(n,t)分别位于直线x=1的两侧,
上为减函数,相应的函数值为(0,1),由题意函数f(x)的图象与直线y=t有两个不同的交点,故有t∈(0,1),易知A(m,t),B(n,t)分别位于直线x=1的两侧,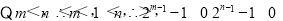
又A,B两点的坐标满足方程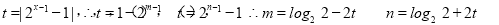
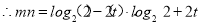
(3)当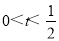 时,
时,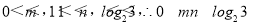
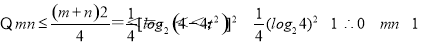
当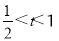 时,
时,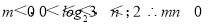 综上mn的取值范围为
综上mn的取值范围为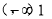 .
.
考点:函数的图象;函数单调性的性质.


科目:高中数学 来源:2014-2015学年浙江省杭州地区7校高三上学期期末模拟联考文科数学试卷(解析版) 题型:选择题
设 是定义在R上的周期为3的函数,当
是定义在R上的周期为3的函数,当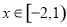 时,
时,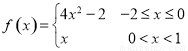 ,则
,则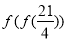 =( )
=( )
A.-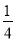 B.
B.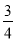 C.
C. D.0
D.0
查看答案和解析>>
科目:高中数学 来源:2014-2015学年稳派新课程高三2月精品文科数学试卷(解析版) 题型:选择题
在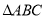 中,内角
中,内角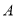 ,
,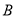 ,
,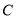 所对应的边分别为
所对应的边分别为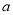 ,
, ,
,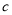 ,若
,若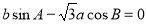 ,且
,且 ,则
,则 的值为( )
的值为( )
A.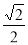 B.
B.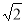 C.2 D.4
C.2 D.4
查看答案和解析>>
科目:高中数学 来源:2014-2015学年稳派新课程高三2月精品理科数学试卷(解析版) 题型:选择题
执行图中的程序框图(其中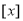 表示不超过
表示不超过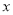 的最大整数),则输出的
的最大整数),则输出的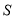 值为( )
值为( )
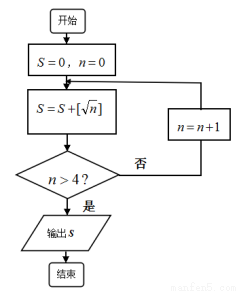
A.4 B.5 C.6 D.7
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市长宁区高三上学期教学质量检测文科数学试卷(解析版) 题型:填空题
已知数列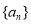 是以
是以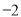 为公差的等差数列,
为公差的等差数列,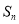 是其前
是其前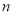 项和,若
项和,若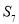 是数列
是数列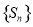 中的唯一最大项,则数列
中的唯一最大项,则数列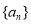 的首项
的首项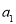 的取值范围是 .
的取值范围是 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年陕西省高三教学质量检测一理科数学试卷(解析版) 题型:选择题
如图,给出的是计算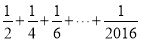 的值的程序框图,其中判断框内应填入的是( )
的值的程序框图,其中判断框内应填入的是( )

A.
B.
C.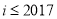
D.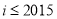
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com