
【题目】已知二次函数![]() 满足
满足![]() (
(![]() ),且
),且![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有唯一实数根,求实数
上有唯一实数根,求实数![]() 的取值范围(注:相等的实数根算一个).
的取值范围(注:相等的实数根算一个).
(3)函数![]() ,试问是否存在实数
,试问是否存在实数![]() ,使得对任意
,使得对任意![]() ,
, ![]() 都有
都有![]() 成立,若存在,求出实数
成立,若存在,求出实数![]() 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)答案见解析.
;(3)答案见解析.
【解析】试题分析:(1)设![]() (
(![]() ),代入条件化简并根据恒等式成立条件得
),代入条件化简并根据恒等式成立条件得![]() ,
, ![]() ,
, ![]() ,(2)研究二次方程根的情况,往往结合二次函数图像,即转化为研究直线与二次函数交点个数,作出图像,根据图像得实数
,(2)研究二次方程根的情况,往往结合二次函数图像,即转化为研究直线与二次函数交点个数,作出图像,根据图像得实数![]() 的取值范围(3)先将不等式恒成立问题转化为对应函数最值:
的取值范围(3)先将不等式恒成立问题转化为对应函数最值: ![]() ,再根据二次函数对称轴与定义区间位置关系,分类讨论函数最值,解对应不等式,可得实数
,再根据二次函数对称轴与定义区间位置关系,分类讨论函数最值,解对应不等式,可得实数![]() 的取值范围
的取值范围
试题解析:(1)设![]() (
(![]() )
)
代入![]() 得
得![]() 对于
对于![]() 恒成立,故
恒成立,故![]()
又由![]() 得
得![]() ,解得
,解得![]() ,
, ![]() ,
, ![]() ,
,
所以![]()
(2)由方程![]() 得
得![]() ,令
,令![]() ,
, ![]() ,
,
即要求函数![]() 在
在![]() 上有唯一的零点,
上有唯一的零点,
①![]() ,则
,则![]() ,代入原方程得
,代入原方程得![]() 或
或![]() ,不合题意;
,不合题意;
②若![]() ,则
,则![]() ,代入原方程得
,代入原方程得![]() 或
或![]() ,满足题意,故
,满足题意,故![]() 成立;
成立;
③若![]() ,则
,则![]() ,代入原方程得
,代入原方程得![]() ,满足题意,故
,满足题意,故![]() 成立.
成立.
④若![]() 且
且![]() 且
且![]() 时,由
时,由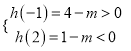 得
得![]() .
.
综上,实数![]() 的取值范围是
的取值范围是![]() .
.
解法2:由方程![]() 得
得![]() ,即直线
,即直线![]() 与函数
与函数![]() ,
, ![]() 的图象有且只有一个交点(参照给分)
的图象有且只有一个交点(参照给分)
(3)由题意知![]()
假设存在实数![]() 满足条件,对任意
满足条件,对任意![]() ,
, ![]() 都有
都有![]() 成立,即
成立,即![]() ,故有
,故有![]() ,
,
由![]() ,
, ![]()
①当![]() 时,
时, ![]() 在
在![]() 上为增函数
上为增函数![]() ,
, ![]() ,所以
,所以![]()
②当![]() 时,
时, ![]()
![]() ,即
,即![]()
解得![]() ,所以
,所以![]() .
.
③当![]() 时,
时, ![]()
即![]() 解得
解得![]() ,所以
,所以![]()
③当![]() 时,
时, ![]()
即![]() ,所以
,所以![]()
综上所述, ![]()
所以当![]() 时,使得对任意
时,使得对任意![]() ,
, ![]() 都有
都有![]() 成立
成立


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】某科考试中,从甲、乙两个班级各抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于90分为及格.
(Ⅰ)设甲、乙两个班所抽取的10名同学成绩方差分别为![]() 、
、![]() ,比较
,比较![]() 、
、![]() 的大小(直接写出结果,不写过程);
的大小(直接写出结果,不写过程);
(Ⅱ)从甲班10人任取2人,设这2人中及格的人数为X,求X的分布列和期望;
(Ⅲ)从两班这20名同学中各抽取一人,在已知有人及格的条件下,求抽到乙班同学不及格的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是偶函数.
是偶函数.
(1)求![]() 的值;
的值;
(2)若函数![]() 的图象与直线
的图象与直线![]() 没有交点,求b的取值范围;
没有交点,求b的取值范围;
(3)设![]() ,若函数
,若函数![]() 与
与![]() 的图象有且只有一个公共点,求实数a的取值范围.
的图象有且只有一个公共点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,AC∩BD=E,AD=2,AB=2![]() ,BC=6,求证:平面PBD⊥平面PAC.
,BC=6,求证:平面PBD⊥平面PAC.
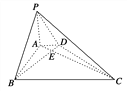
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+1,x∈R.
(1)分别计算f(1)-f(-1),f(2)-f(-2),f(3)-f(-3)的值;
(2)由(1)你发现了什么结论?并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]()
![]() (t+1)lnx,,其中t∈R.
(t+1)lnx,,其中t∈R.
(1)若t=1,求证:当x>1时,f(x)>0成立;
(2)若t>![]() ,判断函数g(x)=x[f(x)+t+1]的零点的个数.
,判断函数g(x)=x[f(x)+t+1]的零点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有甲、乙两种商品,经营销售这两种商品所得的利润依次为M万元和N万元,它们与投入资金![]() 万元的关系可由经验公式给出:M=
万元的关系可由经验公式给出:M=![]() ,N=
,N=![]() (
(![]() ≥1).今有8万元资金投入经营甲、乙两种商品,且乙商品至少要求投资1万元,
≥1).今有8万元资金投入经营甲、乙两种商品,且乙商品至少要求投资1万元,
设投入乙种商品的资金为![]() 万元,总利润
万元,总利润![]() ;
;
(2)为获得最大利润,对甲、乙两种商品的资金投入分别是多少?共能获得多大利润?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com