Question

18．已知双曲线C：$\frac{{y}^{2}}{{a}^{2}}-\frac{{x}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的离心率e=$\frac{\sqrt{5}}{2}$，点P是抛物线y²=4x上的一个动点，P到双曲线C的上焦点F₁（0，c）的距离与到直线x=-1的距离之和的最小值为$\sqrt{6}$，则该双曲线的方程为（　　）

• A． $\frac{{y}^{2}}{2}-\frac{{x}^{2}}{3}$=1
• B． y²-$\frac{{x}^{2}}{4}$=1
• C． $\frac{{y}^{2}}{4}$-x²=1
• D． $\frac{{y}^{2}}{3}-\frac{{x}^{2}}{2}$=1

Answer 1

分析 由题意可知：P到准线的距离即为P到焦点的距离为|PF|，可得|PF|+|PF₁|的最小值为$\sqrt{6}$，当P，F，F₁三点共线，可得最小值|FF₁|=$\sqrt{1+{c}^{2}}$=$\sqrt{6}$，即可求得c，根据椭圆的离心率即可求得a和b的值，求得双曲线方程．

解答 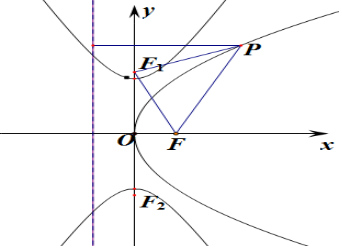解：抛物线y²=4x的焦点F（1，0），准线的方程为x=-1，
曲线C：$\frac{{y}^{2}}{{a}^{2}}-\frac{{x}^{2}}{{b}^{2}}$=1的离心率e=$\frac{c}{a}$=$\frac{\sqrt{5}}{2}$，
由P到双曲线C的上焦点F₁（0，c）的距离与到直线x=-1的距离之和的最小值为$\sqrt{6}$，
由抛物线的定义可得P到准线的距离即为P到焦点的距离为|PF|，
可得|PF|+|PF₁|的最小值为$\sqrt{6}$，
当P，F，F₁三点共线，可得最小值|FF₁|=$\sqrt{1+{c}^{2}}$=$\sqrt{6}$，
即有c=$\sqrt{5}$，
由c²=a²+b²，
解得a=2，b=1，
即有双曲线的方程为$\frac{{y}^{2}}{4}$-x²=1．
故选：C．

点评 本题考查双曲线的简单几何性质，抛物线的定义，考查数形结合思想的应用，属于中档题．