
分析 (Ⅰ)由椭圆经过点($\frac{2}{3},\frac{{2\sqrt{6}}}{3}$),且其左焦点坐标为(-1,0),求出a,b,c,由此能求出椭圆的方程.
(Ⅱ)当直线l1,l2中有一条直线的斜率不存在时,|MN|+|PQ|=7;当直线l1的斜率存在且不为0时,设直线l1的方程y=k(x-1),代入椭圆方程,得(3+4k2)x2-8k2x+4k2-12=0,由此利用韦达定理、弦长公式求出|MN|,设直线l2的方程为y=-$\frac{1}{k}$(x-1),同理得:|PQ|=$\frac{12(1+{k}^{2})}{4+3{k}^{2}}$,由此能求出|MN|+|PQ|的最小值.
解答 解:(Ⅰ)∵椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$经过点($\frac{2}{3},\frac{{2\sqrt{6}}}{3}$),且其左焦点坐标为(-1,0),
∴c=1,2a=$\sqrt{\frac{25}{9}+\frac{24}{9}}$+$\sqrt{\frac{1}{9}+\frac{24}{9}}$=4,∴b=$\sqrt{{a}^{2}-{c}^{2}}$=$\sqrt{3}$,
∴椭圆的方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$. …(4分)
(Ⅱ)①当直线l1,l2中有一条直线的斜率不存在时,|MN|+|PQ|=7.…(5分)
②当直线l1的斜率存在且不为0时,设直线l1的方程y=k(x-1),设M(x1,y1),N(x2,y2),
由$\left\{\begin{array}{l}{y=k(x-1)}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,得(3+4k2)x2-8k2x+4k2-12=0,
∴${x}_{1}+{x}_{2}=\frac{8{k}^{2}}{3+4{k}^{2}}$,${x}_{1}{x}_{2}=\frac{4{k}^{2}-12}{3+4{k}^{2}}$,
|MN|=$\sqrt{(1+{k}^{2})({x}_{1}-{x}_{2})^{2}}$=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\frac{12(1+{k}^{2})}{3+4{k}^{2}}$,
设直线l2的方程为y=-$\frac{1}{k}$(x-1),同理得:|PQ|=$\frac{12(1+{k}^{2})}{4+3{k}^{2}}$,
所以|MN|+|PQ|=$\frac{84({k}^{2}+1)^{2}}{(4+3{k}^{2})(3+4{k}^{2})}$,…(9分)
设t=k2+1,则t>1,所以$\frac{1}{t}=\frac{1}{2}$时,|MN|+|PQ|有最小值$\frac{48}{7}<7$.
综上,|MN|+|PQ|的最小值是$\frac{48}{7}$.…(12分)
点评 本题考查椭圆方程的求法,考查两线段和的最小值的求法,是中档题,解题时要认真审题,注意椭圆性质、韦达定理、弦长公式的合理运用.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:解答题
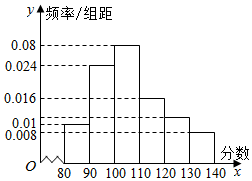 某校在2 015年11月份的高三期中考试后,随机地抽取了50名学生的数学成绩并进行了分析,结果这50名同学的成绩全部介于80分到140分之间.现将结果按如下方式分为6组,第一组[80,90),第二组[90,100),…第六组[130,140],得到如图所示的频率分布直方图.
某校在2 015年11月份的高三期中考试后,随机地抽取了50名学生的数学成绩并进行了分析,结果这50名同学的成绩全部介于80分到140分之间.现将结果按如下方式分为6组,第一组[80,90),第二组[90,100),…第六组[130,140],得到如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
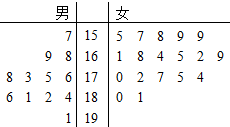 某小学对五年级的学生进行体质测试,已知五年一班共有学生30人,测试立定跳远的成绩用茎叶图表示如图(单位:cm):
某小学对五年级的学生进行体质测试,已知五年一班共有学生30人,测试立定跳远的成绩用茎叶图表示如图(单位:cm):查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{10}$ | B. | $\frac{9}{20}$ | C. | $\frac{6}{35}$ | D. | $\frac{9}{35}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com