
【题目】已知二次函数f(x)=x2+ax+b(a,b∈R)的定义域为[-1,1],且|f(x)|的最大值为M.
(1)证明:|1+b|≤M;
(2)证明:M≥![]() .
.
科目:高中数学 来源: 题型:
【题目】某数学教师对所任教的两个班级各抽取20名学生进行测试,分数分布如表:
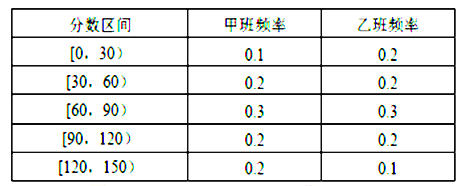
(1)若成绩120分以上(含120分)为优秀,求从乙班参加测试的90分以上(含90分)的同学中,随机任取2名同学,恰有1人为优秀的概率;
(2)根据以上数据完成下面的![]() 列联表:在犯错概率小于
列联表:在犯错概率小于![]() 的前提下,你是否有足够的把握认为学生的数学成绩是否优秀与班级有关系?
的前提下,你是否有足够的把握认为学生的数学成绩是否优秀与班级有关系?

| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
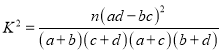 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x-1|+|x-2a|.
(1)当a=1时,求f(x)≤3的解集;
(2)当x∈[1,2]时,f(x)≤3恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为自然对数的底数,
为自然对数的底数,![]() ),
),![]() (
(![]() ,
,![]()
![]() ),
),
⑴若![]() ,
,![]() .求
.求![]() 在
在![]() 上的最大值
上的最大值![]() 的表达式;
的表达式;
⑵若![]() 时,方程
时,方程![]() 在
在![]() 上恰有两个相异实根,求实根
上恰有两个相异实根,求实根![]() 的取值范围;
的取值范围;
⑶若![]() ,
,![]() ,求使
,求使![]() 得图像恒在
得图像恒在![]() 图像上方的最大正整数
图像上方的最大正整数![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在极坐标系中点C的极坐标为![]() .
.
(1)求出以点C为圆心,半径为2的圆的极坐标方程(写出解题过程)并画出图形;
(2)在直角坐标系中,以圆C所在极坐标系的极点为原点,极轴为x轴的正半轴建立直角坐标系,点P是圆C上任意一点,Q(5,-![]() ),M是线段PQ的中点,当点P在圆C上运动时,求点M的轨迹的普通方程.
),M是线段PQ的中点,当点P在圆C上运动时,求点M的轨迹的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过研究学生的学习行为,心理学家发现,学生接受能力依赖于老师引入概念和描述问题所用的时间,讲座开始时,学生的兴趣激增,中间有一段不太长的时间,学生的兴趣保持理想的状态,随后学生的注意力开始分散,分析结果和实验表明,用![]() 表示学生掌握和接受概念的能力(
表示学生掌握和接受概念的能力(![]() 的值越大,表示接受能力越强),
的值越大,表示接受能力越强),![]() 表示提出和讲授概念的时间(单位:分),可以有以下公式:
表示提出和讲授概念的时间(单位:分),可以有以下公式: 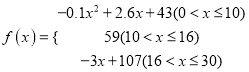 .
.
(1)开讲多少分钟后,学生的接受能力最强?能维持多少分钟?
(2)开讲5分钟与开讲20分钟比较,学生的接受能力何时强一些?
(3)一个数学难题,需要55的接受能力以及13分钟的时间,老师能否及时在学生一直达到所需接受能力的状态下讲授完这个难题?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:①集合![]() 的子集个数有16个;②定义在
的子集个数有16个;②定义在![]() 上的奇函数
上的奇函数![]() 必满足
必满足![]() ;③
;③![]() 既不是奇函数又不是偶函数;④偶函数的图像一定与
既不是奇函数又不是偶函数;④偶函数的图像一定与![]() 轴相交;⑤
轴相交;⑤![]() 在
在![]() 上是减函数。
上是减函数。
其中真命题的序号是 ______________(把你认为正确的命题的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①若(1-x)5=a0+a1x+a2x2+a3x3+a4x4+a5x5,则|a1|+|a2|+|a3|+|a4|+|a5|=32
②α,β,γ是三个不同的平面,则“γ⊥α,γ⊥β”是“α∥β”的充分条件
③已知sin![]() =
=![]() ,则cos
,则cos![]() =
=![]() .其中正确命题的个数为( )
.其中正确命题的个数为( )
A.0 B.1
C.2 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com