
【题目】已知函数![]() (
(![]() 为自然对数的底数,
为自然对数的底数,![]() ),
),![]() (
(![]() ,
,![]()
![]() ),
),
⑴若![]() ,
,![]() .求
.求![]() 在
在![]() 上的最大值
上的最大值![]() 的表达式;
的表达式;
⑵若![]() 时,方程
时,方程![]() 在
在![]() 上恰有两个相异实根,求实根
上恰有两个相异实根,求实根![]() 的取值范围;
的取值范围;
⑶若![]() ,
,![]() ,求使
,求使![]() 得图像恒在
得图像恒在![]() 图像上方的最大正整数
图像上方的最大正整数![]() .
.
【答案】(1)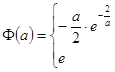
![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)借助题设条件运用分类整合思想求解;(2)依据题设运用化归转化的数学思想进行探求;(3)依据题设构造函数![]() ,运用导数的知识求解.
,运用导数的知识求解.
试题解析:
(1)![]() 时,
时,![]() ,
,
![]() ;
;
①当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为增函数,此时
上为增函数,此时![]() ,
,
②当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为增函数,
上为增函数,
故![]() 在
在![]() 上为增函数,此时
上为增函数,此时![]() …………………………………2分
…………………………………2分
③当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为增函数,在
上为增函数,在![]() 上为减函数,
上为减函数,
若![]() ,即
,即![]() 时,故
时,故![]() 在
在![]() 上为增函数,在
上为增函数,在![]() 上为减函数,
上为减函数,
此时![]() ………………………………5分
………………………………5分
若![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上为增函数,则此时
上为增函数,则此时![]() ,
,
综上所述: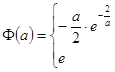
![]() ………………………………6分,
………………………………6分,
(2)![]() ,
,![]() ,
,
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,……………7分
上单调递增,……………7分
![]()
![]() 在
在![]() 上恰有两个相异实根,
上恰有两个相异实根,
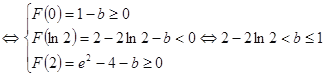 ,
,
![]() 实数
实数![]() 的取值范围是
的取值范围是![]() ,…………………………………10分
,…………………………………10分
(3)由题设:![]() ,
,![]() ,(*)
,(*)
![]() ,故
,故![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]() (*)
(*)![]() ,
,
设![]() ,则
,则![]() ,
,
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,…………………………12分
上单调递减,…………………………12分
而![]() ,
,
且![]() ,
,
故存在![]() ,使
,使![]() ,
,
且![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,
又![]() ,
,![]() ,
,![]() 时,使
时,使![]() 的图像恒在
的图像恒在![]() 图像的上方的最大整数
图像的上方的最大整数![]() ………………14分.
………………14分.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() +
+![]() =1(a>b>0)的左焦点为F,右顶点为A,抛物线y2=
=1(a>b>0)的左焦点为F,右顶点为A,抛物线y2=![]() (a+c)x与椭圆交于B,C两点,若四边形ABFC是菱形,则椭圆的离心率等于( )
(a+c)x与椭圆交于B,C两点,若四边形ABFC是菱形,则椭圆的离心率等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2=4,直线l:x+y=2.以O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系.
(1)将圆C和直线l的方程化为极坐标方程;
(2)P是l上的点,射线OP交圆C于点R,又点Q在OP上且满足|OQ|·|OP|=|OR|2,当点P在l上移动时,求点Q轨迹的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记![]() 表示
表示![]() 中的最大值,如
中的最大值,如![]() ,已知函数
,已知函数![]() .
.
(1)求函数![]() 在
在![]() 上的值域;
上的值域;
(2)试探讨是否存在实数![]() , 使得
, 使得![]() 对
对![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的取值范围;
的取值范围;
若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=x2+ax+b(a,b∈R)的定义域为[-1,1],且|f(x)|的最大值为M.
(1)证明:|1+b|≤M;
(2)证明:M≥![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.
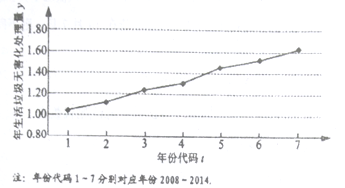
(1)由折线图看出,可用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)建立![]() 关于
关于![]() 的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
参考数据: ![]() ,
, ![]() ,
, 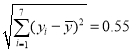 ,
, ![]() .
.
参考公式:相关系数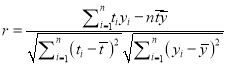
回归方程![]() 中,
中, 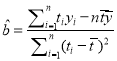 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】比较下列各组中两个值的大小 :
(1)ln0.3,ln2; (2)loga3.1,loga5.2(a>0,且a≠1);
(3)log30.2,log40.2; (4)log3π,logπ3.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com