
如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4.设圆C的半径为1,圆心在l上.
(1)若圆心C也在直线y=x-1上,过点A作圆C的切线,求切线的方程;
(2)若圆C上存在点M,使MA=2MO,求圆心C的横坐标a的取值范围.
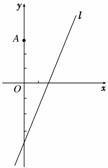
解:(1)由题设,圆心C是直线y=2x-4和y=x-1的交点,解得点C(3,2),于是切线的斜率必存在.设过A(0,3)的圆C的切线方程为y=kx+3,
由题意,得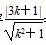 =1,解得k=0或-
=1,解得k=0或-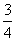 ,
,
故所求切线方程为y=3或3x+4y-12=0.
(2)因为圆心在直线y=2x-4上,所以圆C的方程为(x-a)2+[y-2(a-2)]2=1.
设点M(x,y),因为MA=2MO,
所以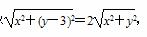
化简得x2+y2+2y-3=0,即x2+(y+1)2=4,所以点M在以D(0,-1)为圆心,2为半径的圆上.由题意,点M(x,y)在圆C上,所以圆C与圆D有公共点,则|2-1|≤CD≤2+1,即1≤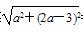 ≤3.
≤3.
由5a2-12a+8≥0,得a∈R;
由5a2-12a≤0,得0≤a≤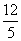 .
.
所以点C的横坐标a的取值范围为[0,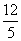 .]
.]


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
某市居民自来水收费标准如下:每户每月用水不超过4t时,每吨为1.80元,当用水超过4t时,超过部分每吨3.00元,某月甲、乙两户共交水费y元,已知甲、乙两户该月用水量分别为5xt、3xt.
(1)求y关于x的函数;
(2)若甲、乙两户该月共交水费26.4元,分别求出甲、乙两户该月的用水量和水费.
查看答案和解析>>
科目:高中数学 来源: 题型:
设P是双曲线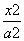 -
-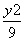 =1上一点,双曲线的一条渐近线方程为3x-2y=0,F1,F2分别是双曲线的左,右焦点,若|PF1|=3,则|PF2|=( )
=1上一点,双曲线的一条渐近线方程为3x-2y=0,F1,F2分别是双曲线的左,右焦点,若|PF1|=3,则|PF2|=( )
A.1或5 B.6
C.7 D.9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com