
【题目】已知函数![]() .
.
(1)当a=1时,x0∈[1,e]使不等式f(x0)≤m,求实数m的取值范围;
(2)若在区间(1,+∞)上,函数f(x)的图象恒在直线y=2ax的下方,求实数a的取值范围.
【答案】(I)![]() (II)
(II)![]()
【解析】试题分析:(I)将a的值代入f(x),求出f(x)的导函数;,将x0∈[1,e]使不等式f(x0)≤m转化为f(x)的最小值小于等于m,利用[1,e]上的函数递增,求出f(x)的最小值,令最小值小于等于m即可.
(II)将图象的位置关系转化为不等式恒成立;通过构造函数,对新函数求导,对导函数的根与区间的关系进行讨论,求出新函数的最值,求出a的范围.
试题解析:解:(I)当a=1时,![]() ,
,
![]()
可知当x∈[1,e]时f(x)为增函数,
最小值为![]() ,
,
要使x0∈[1,e]使不等式f(x0)≤m,即f(x)的最小值小于等于m,
故实数m的取值范围是![]()
(2)已知函数![]() .
.
若在区间(1,+∞)上,函数f(x)的图象恒在直线y=2ax的下方,
等价于对任意x∈(1,+∞),f(x)<2ax,
即![]() 恒成立.
恒成立.
设![]() .
.
即g(x)的最大值小于0.![]()
(1)当![]() 时,
时,![]() ,
,
∴![]() 为减函数.
为减函数.
∴g(1)=﹣a﹣![]() ≤0
≤0
∴a≥﹣![]()
∴![]()
(2)a≥1时,![]() .
.
![]() 为增函数,
为增函数,
g(x)无最大值,即最大值可无穷大,故此时不满足条件.
(3)当![]() 时,g(x)在
时,g(x)在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,
上为增函数,
同样最大值可无穷大,不满足题意.综上.实数a的取值围是![]() .
.


科目:高中数学 来源: 题型:
【题目】一个匀速旋转的摩天轮每12分钟转一周,最低点距地面2米,最高点距地面18米,P是摩天轮轮周上一定点,从P在最低点时开始计时,则16分钟后P点距地面的高度是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)=(a+1)x﹣2+1(a>0)的图象恒过定点A,且点A又在函数 ![]() 的图象上.
的图象上.
(1)求实数a的值;
(2)解不等式f(x)< ![]() ;
;
(3)函数h(x)=|g(x+2)﹣2|的图象与直线y=2b有两个不同的交点时,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边长分别是a,b,c.满足2acosC+ccosA=b.
(Ⅰ)求角C的大小;
(Ⅱ)求sinAcosB+sinB的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数  .
.
(1)请在直角坐标系中画出函数f(x)的图象,并写出该函数的单调区间;
(2)若函数g(x)=f(x)﹣m恰有3个不同零点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空间四边形ABCD中,AD=BC=2,E,F分别是AB,CD的中点,EF= ![]() ,则异面直线AD,BC所成的角的补角为( )
,则异面直线AD,BC所成的角的补角为( ) 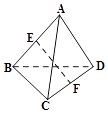
A.120°
B.60°
C.90°
D.30°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设{an}是各项都为正数的等比数列,{bn}是等差数列,且a1=b1=1,a3+b5=13,a5+b3=21.
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)设数列{an}的前n项和为Sn , 求数列{Snbn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com