
将边长为2,锐角为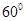 的菱形
的菱形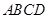 沿较短对角线
沿较短对角线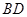 折成二面角
折成二面角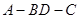 ,点
,点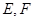 分别为
分别为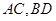 的中点,给出下列四个命题:
的中点,给出下列四个命题:
①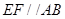 ;②
;②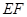 是异面直线
是异面直线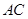 与
与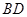 的公垂线;③当二面角
的公垂线;③当二面角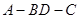 是直二面角时,
是直二面角时,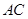 与
与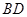 间的距离为
间的距离为 ;④
;④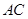 垂直于截面
垂直于截面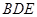 .
.
其中正确的是 (将正确命题的序号全填上).
②③④
解析试题分析:画出图形,利用翻折前后线面关系,角的关系,逐一分析各个选项的正确性,把正确的选项找出来解:如图: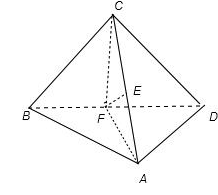
由题意得,EF与AB是异面直线,故①不正确.由等腰三角形的中线性质得 CF⊥BD,AF⊥BD,DB⊥面ACF,又EF?面ACF,∴EF⊥BD,在等腰三角形AFC中,EF⊥AC即直线EF是异面直线AC与BD的公垂线,故②正确.当二面角A-BD-C是直二面角时,则∠CFA=90°,由于 FA=FC= ,且AC=
,且AC=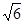 ,EF是等腰三角形FAC的底边上的中线,∴EF⊥AC,EF=
,EF是等腰三角形FAC的底边上的中线,∴EF⊥AC,EF=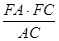 =
= 当二面角A-BD-C是直二面角时,即AC与BD间的距离为
当二面角A-BD-C是直二面角时,即AC与BD间的距离为 ,故③正确.由DB⊥面ACF 得,DB⊥AC,又EF⊥AC,∴AC⊥面EBD,故④正确.故答案为 ②③④.
,故③正确.由DB⊥面ACF 得,DB⊥AC,又EF⊥AC,∴AC⊥面EBD,故④正确.故答案为 ②③④.
考点:棱锥的结构特征
点评:本题考查棱锥的结构特征,注意在翻折过程中哪些量发生了变化,哪些量没有发生变化;位于折线同侧的元素关系不变,位于折线两侧的元素关系会发生变化.


科目:高中数学 来源: 题型:填空题
已知: 是不同的直线,
是不同的直线, 是不同的平面,给出下列五个命题:
是不同的平面,给出下列五个命题:
①若 垂直于
垂直于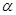 内的两条直线,则
内的两条直线,则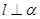 ;
;
②若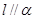 ,则
,则 平行于
平行于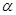 内的所有直线;
内的所有直线;
③若 且
且 则
则 ;
;
④若 且
且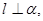 则
则 ;
;
⑤若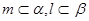 且
且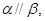 则
则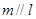 .其中正确命题的序号是
.其中正确命题的序号是
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
将正方形ABCD沿对角线BD折成直二面角 ,有如下四个结论:
,有如下四个结论:
①AC⊥BD;② 是等边三角形;③
是等边三角形;③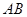 与
与 所成的角为
所成的角为 ;④
;④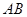 与平面
与平面 成
成 的角。
的角。
其中正确的结论的序号是 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com