练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知，,的夹角为60o, , ,当实数为何值时，⑴∥   ⑵

    ⑴ ⑵

    解析试题分析：，,的夹角为，
    ⑴∥，所以设
    ⑵

    考点：向量的数量积运算及位置关系
    点评：若两向量共线，则满足，若两向量垂直，则

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    已知椭圆：()过点，其左、右焦点分别为，且．
    （1）求椭圆的方程；
    （2）若是直线上的两个动点，且，则以为直径的圆是否过定点？请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    在平面直角坐标系中，以为始边，角的终边与单位圆的交点在第一象限，已知.
    （1）若，求的值；
    （2）若点横坐标为，求.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    平面直角坐标系xOy内有向量＝(1,7)，＝(5,1)，＝(2,1)，点Q为直线OP上一动点．
    (1)当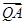·取得最小值时，求坐标；
    (2)当点Q满足(1)中条件时，求cos∠AQB的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知向量，定义函数
    （1）求函数的表达式，并指出其最大最小值；
    （2）在锐角中，角A，B，C的对边分别为a，b，c，且求 的面积S。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    设是平面上的两个向量，若向量与相互垂直，
    （Ⅰ）求实数的值；
    （Ⅱ）若，且，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知,
    (1)求的值；
    （2）求的夹角；
    （3）求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    设
    （Ⅰ）若，求实数的值；
    （Ⅱ）求在方向上的正射影的数量．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    (本小题满分12分)
    A﹑B﹑C是直线上的三点，向量﹑﹑满足：-[y+2]·+ln(x+1)·= ；
    （Ⅰ）求函数y=f(x)的表达式；
    （Ⅱ）若x＞0, 证明f(x)＞；
    （Ⅲ）当时,x及b都恒成立，求实数m的取值范围。

    查看答案和解析>>

    同步练习册答案