Question

(本小题满分12分)
A﹑B﹑C是直线上的三点，向量﹑﹑满足：-[y+2]·+ln(x+1)·= ；
（Ⅰ）求函数y=f(x)的表达式；
（Ⅱ）若x＞0, 证明f(x)＞；
（Ⅲ）当时,x及b都恒成立，求实数m的取值范围。

Answer 1

（I）f(x)=ln(x+1)；(Ⅱ)令g(x)=f(x)－,由，
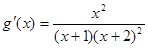∵x>0∴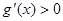∴g(x)在 (0,+∞)上是增函数,故g(x)>g(0)=0,即f(x)> ;
（III）m≤-3或m≥3.

解析试题分析：（I）由三点共线知识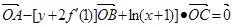，∵,∴,∵A﹑B﹑C三点共线，
∴
∴.∴∴，
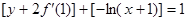
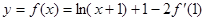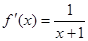∴f(x)=ln(x+1)………………4分
(Ⅱ)令g(x)=f(x)－,由，
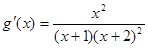∵x>0∴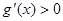∴g(x)在 (0,+∞)上是增函数,故g(x)>g(0)=0,即f(x)> ;…8分
（III）原不等式等价于,
令h(x)= 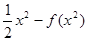=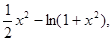由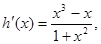
当x∈[-1,1]时,[h(x)]_max="0," ∴m²-2bm-3≥0,令Q(b)= m²-2bm-3，则由Q(1)≥0及Q（-1)≥0解得m≤-3或m≥3. …………12分
考点：本题考查了向量的运算及导函数的运用
点评：，解析几何综合题主要考查直线和圆锥曲线的位置关系以及范围、最值、定点、定值、存在性等问题，近几年高考题中经常出现了以函数、平面向量、导数、数列、不等式、平面几何、数学思想方法等知识为背景，综合考查运用圆锥曲线的有关知识分析问题、解决问题的能力